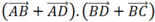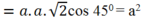Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số phần tử của tập hợp A = { k2 + 1 | k εℤ, |k| \(\le\)2} là:
A. 1
B. 2
C. 3
D. 5

Bài 1. Ta có: \(a\left(a+2\right)\left(a-1\right)^2\ge0\therefore\frac{1}{4a^2-2a+1}\ge\frac{1}{a^4+a^2+1}\)
Thiết lập tương tự 2 BĐT còn lại và cộng theo vế rồi dùng Vasc (https://olm.vn/hoi-dap/detail/255345443802.html)
Bài 5: Bất đẳng thức này đúng với mọi a, b, c là các số thực. Chứng minh:
Quy đồng và chú ý các mẫu thức đều không âm, ta cần chứng minh:
\(\frac{1}{2}\left(a^2+b^2+c^2-ab-bc-ca\right)\Sigma\left[\left(a^2+b^2\right)+2c^2\right]\left(a-b\right)^2\ge0\)
Đây là điều hiển nhiên.

Áp dụng BĐT: \(a^2+b^2\ge2ab\Leftrightarrow2a^2+2b^2\ge a^2+2ab+b^2\Leftrightarrow a^2+b^2\ge\frac{\left(a+b\right)^2}{2}\)
\(f\left(x\right)=x^4+\left(1-x\right)^4\ge\frac{\left[x^2+\left(1-x\right)^2\right]^2}{2}\ge\frac{\left[\frac{\left(x+1-x\right)^2}{2}\right]^2}{2}=\frac{1}{8}\)
Dấu "=" xảy ra \(\Leftrightarrow x=1-x\Leftrightarrow x=\frac{1}{2}\)
Vậy tập giá trị của f(x) là: [1/8;+\(\infty\))

![]()
- LUYỆN TẬP
- HỌC BÀI
- HỎI ĐÁP
- KIỂM TRA
- VINSCHOOL
⋯
MUA THẺ HỌC
- 1
 khoilaba
khoilaba
Hãy xác thực tài khoản để bảo vệ tài khoản của bạn và nhận thưởng VIP từ OLM Xác thực ngay
Giúp tôi giải toán và làm văn
Tìm kiếm
- Mới nhất
- Chưa trả lời
- Câu hỏi hay
- Câu hỏi tôi quan tâm
- Câu hỏi của bạn bè
- Gửi câu hỏi
Tất cảToánTiếng ViệtTiếng Anh

trần bảo khánh linh
Trả lời
3
Đánh dấu
3 phút trước
Helen Keller là ai
Nhanh 3 k nhé
Thank s
Câu hỏi tương tự Đọc thêm Báo cáo
Tiếng Việt lớp 1
![]()
![]() TRẦN TUẦN NAM Vài giây trước
TRẦN TUẦN NAM Vài giây trước
Thống kê hỏi đáp
Báo cáo sai phạm
Helen Adams Keller (27 tháng 6 năm 1880 – 1 tháng 6 năm 1968) là nữ văn sĩ, nhà hoạt động xã hội, diễn giả người Mỹ. Bà là người khiếm thị, khiếm thính đầu tiên giành học vị Cử nhân Nghệ thuật.[1][2
Đúng 0 Sai 0
![]() Emily Nain 1 phút trước
Emily Nain 1 phút trước
Thống kê hỏi đáp
Báo cáo sai phạm
Helen Adams Keller là nữ văn sĩ, nhà hoạt động xã hội, diễn giả người Mỹ. Bà là người khiếm thị, khiếm thính đầu tiên giành học vị Cử nhân Nghệ thuật. Bà được tạp chí Time xếp vào danh sách 100 nhân vật tiêu biểu của thế kỷ 20
#EMNA#
Đúng 0 Sai 0
![]() ︵✿๖ۣۜSɦĭηησʂυƙε↭-↭^^‿✿ 1 phút trước
︵✿๖ۣۜSɦĭηησʂυƙε↭-↭^^‿✿ 1 phút trước
Thống kê hỏi đáp
Báo cáo sai phạm
Helen Adams Keller sinh ra tại Tuscumbia, Alabama. Gia đình bà sống trong khu điền trang Ivy Green[5] được ông nội của bà xây dựng từ những thập kỉ trước.[6]
Cha bà là Arthur H. Keller[7] là người biên tập lâu năm cho tờ báo Tuscumbia North Alabamian và từng là đại úy trong Quân đội miền nam.[6] Bà nội của Helen là chị em họ với Robert E. Lee.[8] Mẹ bà là Kate Adams,[9] là con gái của Charles W. Adams[10] là người gốc từ Massachusetts và từng tham chiến cho Quân đội miền nam trong suốt Cuộc nội chiến Mỹ và trở thành đại tá. Họ nội của Helen thuộc dòng dõi với Casper Keller, người có gốc gác Thụy Sĩ.[8][11]
Keller không bị mù và điếc bẩm sinh[12]. Khi chào đời được khoảng 19 tháng, bà bị ốm nặng sốt cao viêm màng não và không may hỏng mất đôi mắt, và sau đó tai cũng bị điếc. Gia đình bất hạnh chứng kiến đứa con gái vùa lớn lên vừa chống chọi với số phận nghiệt ngã, càng lớn thì tính tình của Keller càng nóng nảy cáu gắt.
Học vấn[sửa | sửa mã nguồn]
Keller và cô Anne Sullivan vào tháng 7 năm 1888
Năm 1886, mẹ bà tình cờ biết được một đứa bé cũng bị mù-điếc như con mình nhưng đã được dạy dỗ thành công, liền tới Baltimore, Maryland gặp bác sĩ để xin lời khuyên. Người bác sĩ này khuyên bà nên tới gặp Alexander Graham Bell, lúc đó còn đang là một nhà chuyên môn chuyên làm việc với những trẻ em bị điếc tại địa phương. Bell lại giới thiệu bà mẹ đưa con gái của mình tới học tại trường Perkins dành cho người mù, tọa lạc tại Nam Boston, tiểu bang Massachusetts. Tại đây Keller đã được gặp cô gia sư Anne Sullivan người Ireland vừa mới tốt nghiệp, người đã từng gần như mất hết thị lực khi mới lên năm tuổi và bắt đầu một tình bạn kéo dài suốt 49 năm trời.
Keller và cô Anne đang học từ
Helen Keller, năm 1904
Helen Keller đang đọc sách với chữ nổi, khoảng năm 1907
Helen Keller
Có một lần Anne tặng cho Keller một con búp bê bằng vải mà cô ôm trên tay. Chờ cho Keller chơi một hồi, Anne liền cầm lấy bàn tay Keller và viết chữ "búp bê" (doll) lên lòng bàn tay em. Keller rất thích thú với cách thể hiện đó, từ đó về sau Anne thường xuyên tập cho Keller ghép chữ cái theo cách này. Sau 3 tháng, thông qua ngôn ngữ động tác tay và sờ xem cử động môi của Anne, Keller đã học được hơn 400 từ đơn cùng một số đoản ngữ.
Năm Keller 8 tuổi, cô Anne đưa bà tới học tại trường Perkins, nơi có các loại sách chữ nổi và các trẻ em bị mù-điếc khác. Chẳng bao lâu, Keller đã bộc lộ rõ tài năng vượt trội về các môn toán, địa lý, sinh học, tập đọc; em còn học cả bơi, chèo thuyền, cưỡi ngựa, đi xe. Sau đó Keller vào học trường nữ học tiểu bang Massachusetts, cô giáo Anne luôn luôn ở bên cạnh Keller để viết lại nội dung bài giảng vào lòng bàn tay Keller. Năm 1900 Keller thi đậu vào trường Radcliffe College (khu mở rộng của Đại học Harvard từ năm 1879 cho sinh viên nữ với các tòa nhà và khuôn viên riêng), học tài liệu chữ nổi dành cho người mù. Cô học nhiều ngoại ngữ, kể cả tiếng Pháp và tiếng Đức, và kiên trì học tới mức khi nào đầu ngón tay rớm máu mới chịu dừng. Số lượng bài vở khổng lồ nhanh chóng làm hỏng thị lực của gia sư Anne. Đến tháng 6 năm 1904 Keller tốt nghiệp và trở thành người mù-điếc đầu tiên được tốt nghiệp đại học.[2] Sau đó, cô được nhận một số học hàm tiến sĩ danh dự, trong số đó có Đại học Harvard.
Hoạt động chính trị[sửa | sửa mã nguồn]
Hai năm sau ngày tốt nghiệp, Keller được vinh dự bầu vào chức chủ tịch hội người mù tiểu bang Massachusetts, bắt tay vào công việc xã hội cụ thể phục vụ cho cộng đồng người mù. Keller đón tiếp rất nhiều người mù, trả lời nhiều thư từ và đi thuyết giảng lưu động tại 39 nước trên thế giới. Cô không quản ngại vất vả, cống hiến hết sức mình cho chương trình giáo dục và chữa trị cho người mù. Năm 1920 với sự phấn đấu không mệt mỏi, Keller đã thành lập được tổ chức quần chúng trên phạm vi toàn quốc của Hội người mù toàn nước Mỹ. Tổ chức này vẫn còn tồn tại cho đến ngày nay.
Keller trở thành một biểu tượng của tinh thần tự lực phi thường khi suốt đời sống trong thế giới không ánh sáng, không âm thanh nhưng vẫn cống hiến hết sức lực nhằm đem niềm vui đến với người tàn tật, có cùng hoàn cảnh như mình. Cô đã được gặp nhiều tổng thống Mỹ như Grover Cleveland, Benjamin Harrison, William McKinley, Theodore Roosevelt, William Howard Taft, Franklin D. Roosevelt, John F. Kennedy... Cô cũng trở thành bạn của những con người nổi tiếng như Alexander Graham Bell, Charlie Chaplin, Mark Twain.
Bà bắt đầu tham gia phong trào xã hội tại nước Mỹ. Keller gia nhập Đảng Xã hội Hoa Kỳ, và về sau bỏ đảng đó để gia nhập Industrial Workers of the World (Công nhân kỹ nghệ của Thế giới). Những nhà báo mà về trước khen ngợi sự can đảm và thông minh của bà bây giờ chỉ ra là bà bị tàn tật. Chủ báo Brooklyn Eagle viết rằng "những sai lầm [của bà] xuất hiện từ những hạn chế rõ ràng khi lớn lên". Keller trả lời chủ báo này, nói đến lần gặp ông trước khi ông biết đến những quan điểm chính trị của bà:
At that time the compliments he paid me were so generous that I blush to remember them. But now that I have come out for socialism he reminds me and the public that I am blind and deaf and especially liable to error. I must have shrunk in intelligence during the years since I met him... Oh, ridiculous Brooklyn Eagle! Socially blind and deaf, it defends an intolerable system, a system that is the cause of much of the physical blindness and deafness which we are trying to prevent.[1]
Bà cũng biểu tình chống chiến tranh và đồng sáng lập tổ chức dân quyền ACLU[2]. Các hoạt động này có liên quan đến quan điểm công bằng của Keller.
Giới thiệu loài chó Akita tới nước Mỹ[sửa | sửa mã nguồn]
Keller tại Nhật Bản năm 1948 trước tượng chó Hachiko
Khi Keller tới thăm tỉnh Akita, Nhật Bản vào tháng 7 năm 1937, bà đã hỏi thăm tới Hachiko, một con chó giống Akita nổi tiếng vì sự trung thành và đã chết từ năm 1935, và bày tỏ ý định muốn có một chú chó như thế. Chỉ trong vòng một tháng, một chú chó tên là Kamikaze-go đã được gửi đến, nhưng sau đó đã chết bệnh quá sớm. Chính phủ Nhật Bản quyết định tặng ch
~Hok tốt~
Đọc tiếp...
Đúng 0 Sai 0

NGUYEN TRUNG KIEN
Trả lời
1
Đánh dấu
4 phút trước
cmr 20a+11b chia het cho 17 khi va chi khi 83a+38b chia het cho 17
Toán lớp 6 Toán chứng minh
![]()
![]() NGUYEN TRUNG KIEN 3 phút trước
NGUYEN TRUNG KIEN 3 phút trước
Thống kê hỏi đáp
Báo cáo sai phạm
giúp mn nha
Đúng 0 Sai 0

JS1_❤❣A.R.M.Y-Jung Hoseok❣❤ [ RBL ] ❧♛☙
Trả lời
6
Đánh dấu
6 phút trước
1 + 1 + 90 = ?
Hãy kể tên 5 bộ anime mà bn thik nhất :)
#JH
Tiếng Anh lớp 5 Đố vui
![]()
![]() ︵✿๖ۣۜSɦĭηησʂυƙε↭-↭^^‿✿ Vài giây trước
︵✿๖ۣۜSɦĭηησʂυƙε↭-↭^^‿✿ Vài giây trước
Thống kê hỏi đáp
Báo cáo sai phạm
1 + 1 + 90 =92
~Hok tốt~
Đúng 0 Sai 0
![]() ︵✿ĐứC̸͟͞ MạN̸͟͞H̸͟͞™➷ ➸ ➹ 2 phút trước
︵✿ĐứC̸͟͞ MạN̸͟͞H̸͟͞™➷ ➸ ➹ 2 phút trước
Thống kê hỏi đáp
Báo cáo sai phạm
=92
bó tay m...

Bài 1:
Áp dụng BĐT Bunhiacopxky ta có:
\((a^2+2c^2)(1+2)\geq (a+2c)^2\)
\(\Rightarrow \sqrt{a^2+2c^2}\geq \frac{a+2c}{\sqrt{3}}\)
\(\Rightarrow \frac{\sqrt{a^2+2c^2}}{ac}\geq \frac{a+2c}{\sqrt{3}ac}=\frac{ab+2bc}{\sqrt{3}abc}\)
Hoàn toàn tương tự: \(\left\{\begin{matrix} \frac{\sqrt{c^2+2b^2}}{bc}\geq \frac{ac+2ab}{\sqrt{3}abc}\\ \frac{\sqrt{b^2+2a^2}}{ab}\geq \frac{bc+2ac}{\sqrt{3}abc}\end{matrix}\right.\)
Cộng theo vế các BĐT trên thu được:
\(\text{VT}\geq \frac{1}{\sqrt{3}}.\frac{ab+2bc+ac+2ab+bc+2ac}{abc}=\frac{1}{\sqrt{3}}.\frac{3(ab+bc+ac)}{abc}=\frac{1}{\sqrt{3}}.\frac{3abc}{abc}=\sqrt{3}\)
Ta có đpcm
Dấu bằng xảy ra khi $a=b=c=3$
Bài 2: Bài này sử dụng pp xác định điểm rơi thôi.
Áp dụng BĐT AM-GM ta có:
\(24a^2+24.(\frac{31}{261})^2\geq 2\sqrt{24^2.(\frac{31}{261})^2a^2}=\frac{496}{87}a\)
\(b^2+(\frac{248}{87})^2\geq 2\sqrt{(\frac{248}{87})^2.b^2}=\frac{496}{87}b\)
\(93c^2+93.(\frac{8}{261})^2\geq 2\sqrt{93^2.(\frac{8}{261})^2c^2}=\frac{496}{87}c\)
Cộng theo vế:
\(B+\frac{248}{29}\geq \frac{496}{87}(a+b+c)=\frac{496}{87}.3=\frac{496}{29}\)
\(\Rightarrow B\geq \frac{496}{29}-\frac{248}{29}=\frac{248}{29}\)
Vậy \(B_{\min}=\frac{248}{29}\). Dấu bằng xảy ra khi: \((a,b,c)=(\frac{31}{261}; \frac{248}{87}; \frac{8}{261})\)
Chọn A.
Theo quy tắc hình bình hành ta có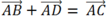
Do đó
(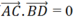 vì AC và BD vuông góc với nhau)
vì AC và BD vuông góc với nhau)
Mặt khác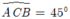 và theo định lý Pitago ta có:
và theo định lý Pitago ta có:
Suy ra