
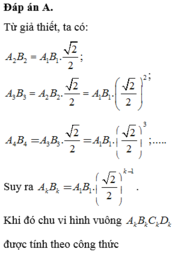
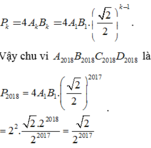
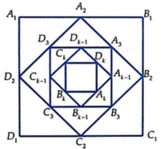
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

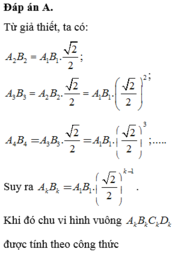
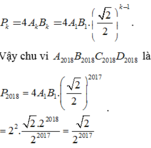


Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1) hay
Kx- y+k=0 .
Phương trình hoành độ giao điểm của C và d là:
x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0
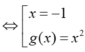
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1
⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠ 9
Khi đó g( x) =0 khi x=2- k ; x = 2 + k Vậy các giao điểm của hai đồ thị lần lượt là
A ( - 1 ; 0 ) ; B ( 2 - k ; 3 k - k k ) ; C ( 2 + k ; 3 k + k k ) .
Tính được
B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .
Khi đó
S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .
Vậy k= 1 thỏa yêu cầu bài toán.
Chọn C.

\(y=\dfrac{2x\left(x-1\right)-2}{x-1}=2x-\dfrac{2}{x-1}\)
tiêm cận y=2 x chia đồ thị thành hai nhánh
=> k< 2 PA(D)

Chọn D.
Phương trình đường thẳng d có hệ số góc k và đi qua I(1; 2) là d: y = k(x - 1) + 2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
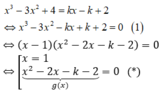
Để d cắt (C) tại ba điểm phân biệt ⇔ Phương trình (*) có hai nghiệm phân biệt x1; x2 khác 1.
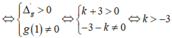
Hơn nữa theo Viet ta có

nên I là trung điểm AB.
Vậy chọn k > -3, hay k ∈ (-3;+∞).

+ Phương trình đường thẳng d có dang d: y= kx-1 .
Phương trình hoành độ giao điểm của đồ thị C và đường thẳng d:
2
x
3
-
3
x
2
-
1
=
k
x
-
1
h
a
y
x
(
2
x
2
-
3
x
-
k
)
=
0
⇔
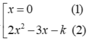
+ Để C cắt d tại ba điểm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt khác 0
⇔ ∆ > 0 0 - k ≠ 0 ⇔ k > - 9 8 k ≠ 0
Vậy chọn k > - 9 8 k ≠ 0
Chọn B.

Phương trình đường thẳng d; y=k(x-1)+2.
Phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d:
x3-3x2+4= k(x-1)+2. Hay x3-3x2-kx+k+2= 0 (1)
⇔
(
x
-
1
)
(
x
2
-
2
x
-
k
-
2
)
=
0
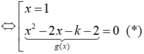
( C) cắt d tại ba điểm phân biệt khi và chỉ khi phương trình có hai nghiệm phân biệt x1; x2 khác 1
⇔ ∆ ' g > 0 g ( 1 ) ≠ 0 ⇔ k + 3 > 0 - 3 - k ≠ 0 ⇔ k > - 3
Hơn nữa theo Viet ta có
x 1 + x 2 = 2 = 2 x I y 1 + y 2 = k ( x 1 + x 2 ) - 2 k + 4 = 4 = 2 y I
nên I là trung điểm AB.
Vậy chọn k> -3, hay k ∈ (-3; +∞). Do đó có vô số giá trị k nguyên thỏa mãn yêu cầu bài toán.
Chọn D.

có
Gắn vào hệ trục Oxyz có
CÓ : S(0,0,0) A(0,0,a) , B(0,a,0), C(a,0,0)
e nhớ ko lầm là a đã học tới bài này âu mà sao bik làm hay z???

+Ta có đạo hàm y’ = 3x2- 6mx+ 3( m+ 1) .
Do K thuộc ( C) và có hoành độ bằng -1, suy ra K( -1; -6m-3)
Khi đó tiếp tuyến tại K có phương trình
∆: y= ( 9m+ 6) x+ 3m+ 3
Đường thẳng ∆ song song với đường thẳng d
⇒ 3 x + y = 0 ⇔ y = - 3 x ⇔ 9 m + 6 = - 3 3 m + 3 ≠ 0 ⇔ m = - 1 m ≠ - 1
Vậy không tồn tại m thỏa mãn đầu bài.
Chọn D.