K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HN
1
PT
1
12 tháng 7 2017
sorry mik năm nay mới lên lớp 7 lên ko thể giúp j cho bạn
CC
4
16 tháng 6 2018
a) Ta có AD là phân giác ^BAC, DE và DF lần lượt vuông góc AB;AC nên DE=DF
Xét \(\Delta\)AFD vuông tại F có ^DAF=1/2^BAC=600 => ^ADF=300
Tương tự tính được: ^ADE=300 = >^ADF+^ADE=^EDF=600
Xét \(\Delta\)DEF: ^EDF=600; DE=DF => \(\Delta\)DEF là tam giác đều.
b) Dễ thấy ^CAM=1800-^BAC=600.
CM // AD => ^ACM=^DAC=1/2^BAC=600
Từ đó suy ra \(\Delta\)ACM là tam giác đều.
c) Do \(\Delta\)ACM đều => CM=AC => CM-CF=CA-CF=AF
=> a - b = AF. Lại có: Tam giác AFD là tam giác nửa đều => AF=1/2AD
=> a - b = 1/2AD => AD= 2(a - b).
Vậy .........
NK
0
CM
8 tháng 6 2018
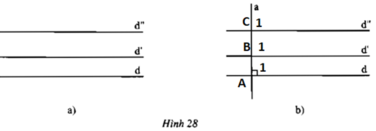
Vì a vuông góc với d ⇒ ∠A1 = 90o
• a có vuông góc với d’
Vì d//d’ ⇒ ∠A1 = ∠B1 ( hai góc đồng vị)
⇒ ∠B1 = 90o
• a có vuông góc với d’’
Vì d//d’’ ⇒ ∠A1 = ∠C1 (hai góc đồng vị)
⇒∠C1 = 90o
• d’ có song song với d’’
Vì ∠B1 = ∠C1 = 90o mà hai góc ở vị trí đồng vị
hình đâu bạn ơi
hình đâu