Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có : – Góc x’Oy’ và góc xOy là hai góc đối đỉnh ⇒ góc xOy = góc x’Oy’ = 90o
– ∠(xOy) và ∠(xOy’) là hai góc kề bù ⇒ ∠(xOy) + ∠(xOy’) = 180o
⇒ (xOy’) = 180o – (xOy) = 180o– 90o = 90o
– ∠(xOy’) và ∠(x’Oy) là hai góc đối đỉnh ⇒ ∠(xOy’) = ∠(x’Oy) = 90o
Khi đó các góc ∠yOx’ ; ∠x’Oy’ ; ∠y’Ox cũng đều là những góc vuông
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 84: Vẽ phác hai đường thẳng a và a’ vuông góc với nhau và viết kí hiệu.Lời giải
+) Do tam giác ABD cân tại D nên DA = DB ( định nghĩa tam giác cân).
Suy ra: D nằm trên đường trung trực của AB. (1)
+) Do tam giác ABC là tam giác đều nên CA = CB
Suy ra: C nằm trên đường trung trực của AB (2)
Từ (1) và (2)suy ra: CD là đường trung trực của AB.
+) Do E là trung điểm của AB nên EA = EB
Suy ra E nằm trên đường trung trực của AB
Suy ra, E nằm trên đường thẳng CD.
Do đó, (B) sai .
Chọn B.
Ta có: b b ' ⊥ a a ' nên b b ' ⊥ A B tại (vì hai điểm và thuộc đường thẳng aa' ) (1)
và M là trung điểm của AB (2)
Từ (1) và (2) suy ra nên bb' là đường trung trực của AB (theo định nghĩa đường trung trực)
Tương tự: aa' là đường trung trực của CD.
I là trung điểm của AB nên IA = IB = 1 2 AB = 1 2 .12 = 6 cm
M thuộc đường trung trực của đoạn thẳng AB nên MB = MA = 10 cm
MI là đường trung trực của AB nên MI ⊥ AB
Suy ra tam giác AMI vuông tại I
Áp dụng định lý Py – ta – go ta có: M A 2 = M I 2 + A I 2
⇒ M I 2 = M A 2 − A I 2 = 10 2 − 6 2 = 64
⇒ M I = 64 = 8 cm
Ta có: MA = MB; AI = BI ; MI cạnh chung
Do đó: Δ A M I = Δ B M I (c – c – c)
Suy ra M A I ^ = M B I ^
Vậy A, B, C đúng và D sai (do MA = MB ≠ MI).
Chọn đáp án D
B là sai vì M và I là 2 điểm trùng nhau
D là sai vì MB=8CM; MA=10CM; MB=10CM nên ko thể là MB=MA=MI mà phải là MA=MB>MI
a) Xét tam giác ABE và tam giác ACD có :
AB = AC ( tam giác Abc cân tại A )
AE = AD
Chung \(\widehat{BAC}\)
\(\Rightarrow\) tam giác ABE = tam giác ACD ( c-g-c )
\(\Rightarrow\hept{\begin{cases}BE=CD\left(đpcm\right)\\\widehat{ABE}=\widehat{ACD}\end{cases}}\)
Mà \(\widehat{ABE}+\widehat{OBC}=\widehat{ACD}+\widehat{OCB}\)
\(\Rightarrow\widehat{OBC}=\widehat{OCB}\)
\(\Rightarrow\) tam giác COB cân tại O \(\Rightarrow OB=OC\left(đpcm\right)\)
c) Xét tam giác AOB và tam giác AOC có :
AB = AC
BO = CO
Chung AO
\(\Rightarrow\) tam giác AOB = tam giác AOC ( c-c-c )
\(\Rightarrow\widehat{BAO}=\widehat{CAO}\)
\(\Rightarrow\) OC là tia phân giác \(\widehat{BAC}\)(1)
Mà tam giác ABC cân tại A (2)
Từ (1) và (2) \(\Rightarrow\)AO là trung trực BC
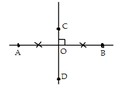
Quan sát hình vẽ đã cho ta thấy
+ AO = OB (D đúng) ⇒ O là trung điểm của AB (1)
+ CD ⊥ AB tại O (2) ⇒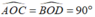
⇒ C đúng
Từ (1) và (2) suy ra CD là đường trung trực của đoạn thẳng AB ⇒ A đúng
+ Vì OC ≠ OD suy ra AB không phải là đường trung trực của CD ⇒ B sai
Chọn đáp án B