Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/
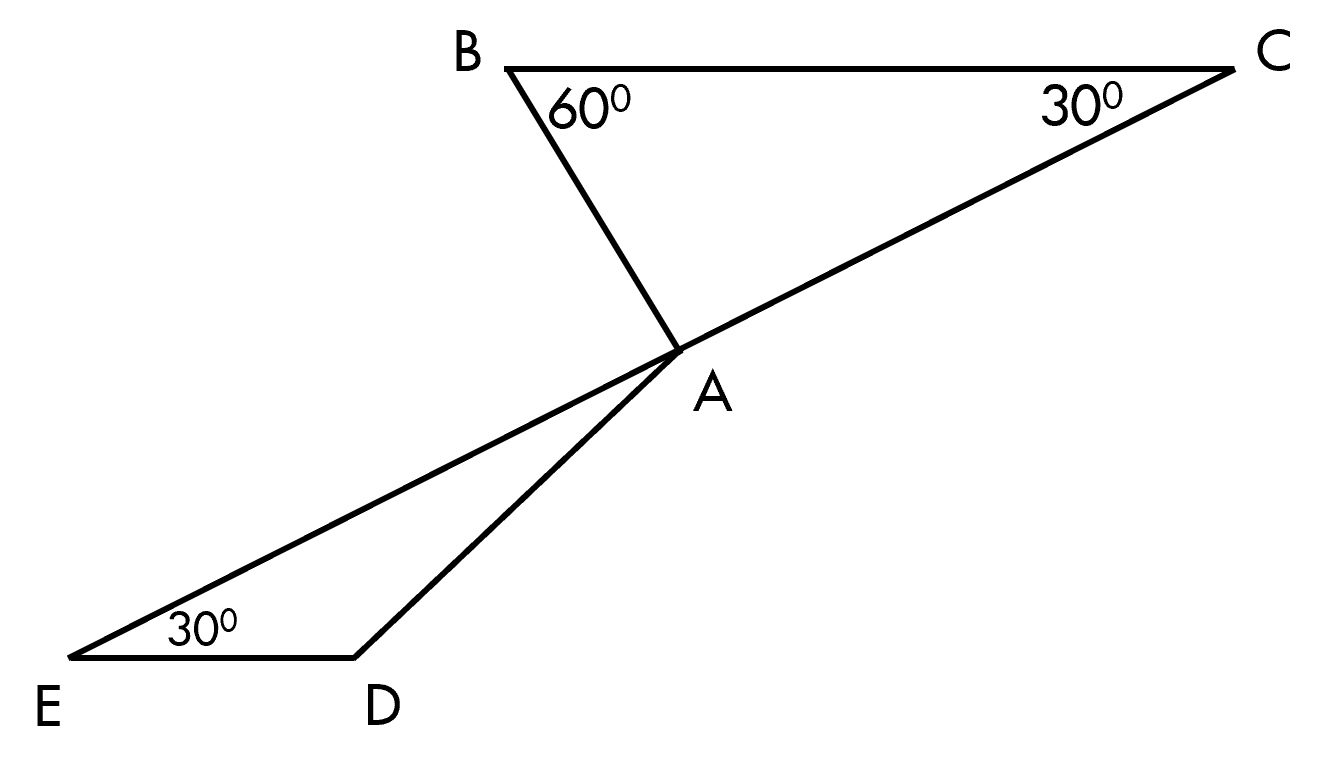
\(\widehat{BCE}=\widehat{CED}=30^o\)
Hai góc trên ở vị trí sole trong => BC//DE
b/
Ta có
BC//DE (cmt) \(\Rightarrow\widehat{AFB}=180^o-\widehat{EDF}\) (Hai góc trong cùng phía bù nhau)
\(\Rightarrow\widehat{AFB}=180^o-135^o=45^o\)

a: Ta có: \(\hat{A_2}+\hat{A_1}=180^0\) (hai góc kề bù)
=>\(\hat{A_2}=180^0-75^0=105^0\)
ta có: \(\hat{A_1}=\hat{A_3}\) (hai góc đối đỉnh)
mà \(\hat{A_1}=75^0\)
nên \(\hat{A_3}=75^0\)
Ta có: \(\hat{A_2}=\hat{A_4}\) (hai góc đối đỉnh)
mà \(\hat{A_2}=105^0\)
nên \(\hat{A_4}=105^0\)
Ta có: \(\hat{B_3}+\hat{B_4}=180^0\) (hai góc kề bù)
=>\(\hat{B_4}=180^0-120^0=60^0\)
ta có: \(\hat{B_3}=\hat{B_1}\) (hai góc đối đỉnh)
mà \(\hat{B_3}=120^0\)
nên \(\hat{B_1}=120^0\)
Ta có: \(\hat{B_4}=\hat{B_2}\) (hai góc đối đỉnh)
mà \(\hat{B_4}=60^0\)
nên \(\hat{B_2}=60^0\)
b: Ta có: \(\hat{xEF}=90^0\)
=>xx'⊥zz' tại E
=>\(\hat{xEz}=\hat{x^{\prime}Ez}=\hat{x^{\prime}EF}=90^0\)
Ta có: \(\hat{yFz^{\prime}}+\hat{y^{\prime}Fz^{\prime}}=180^0\) (hai góc kề bù)
=>\(\hat{yFz^{\prime}}=180^0-110^0=70^0\)
ta có: \(\hat{y^{\prime}Fz^{\prime}}=\hat{yFz}\) (hai góc đối đỉnh)
mà \(\hat{y^{\prime}Fz^{\prime}}=110^0\)
nên \(\hat{yFz}=110^0\)
Ta có: \(\hat{yFz^{\prime}}=\hat{y^{\prime}Fz}\) (hai góc đối đỉnh)
mà \(\hat{yFz^{\prime}}=70^0\)
nên \(\hat{y^{\prime}Fz}=70^0\)

Bài 14:
\(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
\(A\left(x\right)-B\left(x\right)=3x^4+7x^2+8x+2\)
Do đó: \(A\left(x\right)+B\left(x\right)+A\left(x\right)-B\left(x\right)=5x^4-6x^3-3x^2-4+3x^4+7x^2+8x+2\)
=>\(2\cdot A\left(x\right)=8x^4-6x^3+4x^2+8x-2\)
=>\(A\left(x\right)=4x^4-3x^3+2x^2+4x-1\)
Ta có: \(A\left(x\right)+B\left(x\right)=5x^4-6x^3-3x^2-4\)
=>\(B\left(x\right)=5x^4-6x^3-3x^2-4-4x^4+3x^3-2x^2-4x-1\)
=>\(B\left(x\right)=x^4-3x^3-5x^2-4x-5\)
Bài 13:
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
\(f\left(x\right)-g\left(x\right)=4x^4-6x^3+7x^2+8x-9\)
Do đó: \(f\left(x\right)+g\left(x\right)+f\left(x\right)-g\left(x\right)=6x^4-3x^2-5+4x^4-6x^3+7x^2+8x-9\)
=>\(2\cdot f\left(x\right)=10x^4-6x^3+4x^2+8x-14\)
=>\(f\left(x\right)=5x^4-3x^3+2x^2+4x-7\)
\(f\left(x\right)+g\left(x\right)=6x^4-3x^2-5\)
=>\(g\left(x\right)=6x^4-3x^2-5-5x^4+3x^3-2x^2-4x+7=x^4+3x^3-5x^2-4x+2\)

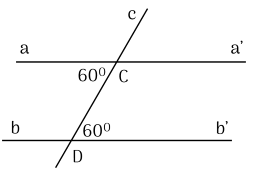
Ta có: góc aCd = góc CDb' (=60°)
Mà 2 góc này ở vị trí so le trong
=> aa' // bb'

(0,5 )2 .4= ( 0,5 . 2 )2 = 12 = 1
( 0,5)3 . 8 = ( 0,5 . 2 )3 = 13 = 1
(0,5)3 . 32 = ( 0,5 . 2 )3 .22 = 13 .22 = 1.4 = 4
( 0,5)6 . 64 = ( 0,5 . 2 )6 = 16 = 1
5, 0,252 .16 = (0,25.4)2 = 12 = 1
6,(0,25)3 .64 = (0,25 .4 )3 = 13 =1
7,(0,2)2 .25 = ( 0,2 .5 )2 = 12 = 1
8,( 0,2 )3 .125 = ( 0,2 . 5 )3 = 13 = 1

Ta có: tia CD nằm giữa hai tia CF và CB
=>\(\hat{BCF}=\hat{BCD}+\hat{FCD}=20^0+50^0=70^0\)
Ta có: \(\hat{BCF}=\hat{ABC}\left(=70^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CF
Ta có: \(\hat{EDC}+\hat{DCF}=130^0+50^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên ED//CF
Ta có: AB//CF
ED//CF
Do đó: AB//DE

Giải:
\(\hat{A}\) + \(\hat{B}\) + \(\hat{C}\) = 180\(^0\) (tổng ba góc trong 1 tam giác)
\(\hat{A}\) = 180\(^0\) - \(\hat{B}-\hat{C}\)
\(\hat{A}\) = 180\(^0\) - \(70^0-30^0\)
\(\hat{A}\) = 110\(^0-30^0\)
\(\hat{A}\) = 80\(^0\)
\(\hat{A}\) = \(D\hat{C}A\)
Mà góc A và góc DCA là hai góc ở vị trí so le trong.
Vậy AB // CD
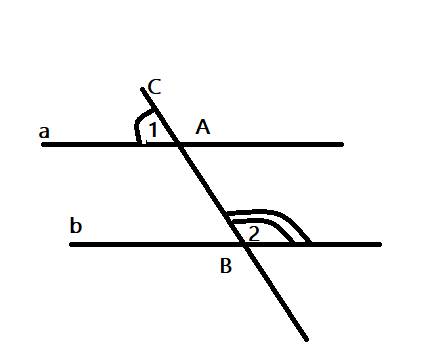





\(\widehat{ABb}=180^o-\widehat{B_2}\) ( vì là hai góc kề bù )
\(\Rightarrow\widehat{ABb}=180^o-108^o=72^o\)
Ta có \(\widehat{A_1}=\widehat{ABb}=72^o\)
mà hai góc ở vị trí đồng vị
\(\Rightarrow a//b\)