Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
a: Xét ΔABC có
M là trung điểm của BA
N la trung điểm của BC
Do đó: MN là đường trung bình
=>MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của DC
Do đó: QP là đường trug bình
=>QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành
b: Xét tứ giác MDPB có
MB//DP
MB=DP
Do đó: MDPB là hình bình hành
c: Xét ΔCDK có
P là trung điểm của CD
PL//DK
DO đó:L là trung điểm của CK
=>CL=LK(1)
Xét ΔALB có
Mlà trung điểm của AB
MK//LB
Do đó:K là trung điểm của AL
=>AK=KL(2)
Từ (1) và (2) suy ra AK=KL=LC

A B C D O M N E F
a) Ta có:
+) M là trung điểm OD
\(\Rightarrow MD=MO=\frac{1}{2}OD\)
N là trung điểm OB
\(\Rightarrow NB=NO=\frac{1}{2}OB\)
Mà OD=OB ( O là giao điểm 2 đường chéo của hình bình hành ABCD)
Suy ra ON=OM=NB=MD (1)
Ta lại có OA=OC
Tứ giác AMCN có hai đường chéo cắt nhau tại trung điểm mỗi đường nên là hình bình hành
b) AMCN là hình bình hành =>NC//AM=> FC//AE mà AF//EC
Vậy suy ra AFCE là hình bình hành
O là trung điểm AC => O là trung điểm EF=> E đối xứng với F qua O
c) AC, BD, EF đều qua O nên đồng quy
d) Xét tam giác DNC có NC//ME
\(\Rightarrow\frac{DE}{EC}=\frac{DM}{MN}\)
Mà DM=OM=ON ( theo 1)
=> \(DM=\frac{1}{2}MN\)
=>\(\frac{DE}{EC}=\frac{DM}{MN}=\frac{1}{2}\Rightarrow DE=\frac{1}{2}EC\)
e) Để hình bình hành AMCN là hình chữ nhật thì MN=AC
Mà \(MN=\frac{1}{2}BD\)nên \(AC=\frac{1}{2}BD\)
Vậy ABCD cần điều kiện là \(AC=\frac{1}{2}BD\)thì AMCN là hình chữ nhật

Hình em tự vẽ nha.
a, ABCD là hình bình hành \(\Rightarrow\)2 đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
Tứ giác AHCK có 2 đường chéo AC và HK tại trung điểm của mỗi đường \(\Rightarrow\)AHCK là hình bình hành
b, AHCK là hình bình hành \(\Rightarrow AH//CK\Leftrightarrow AM//NC\)
Tứ giác AMCN có: \(AN//MC\left(gt\right)\)
\(AM//NC\left(cmt\right)\)
\(\Rightarrow\)AMCN là hình bình hành \(\Rightarrow\)2 đường chéo AC và MN cắt nhau tại trung điểm O của AC \(\Rightarrow\)O là trung điểm của MN

- Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc B17 Tháng mười hai 2013#2 
nhuquynhdatGuest
bài 2
a) AB//CD => AB//CE(1)
Xét tam giác ADE có AH là đg` cao
lại có E đối xứng với D qua H => H là trung điểm của DE => AH là trung tuyến
=> tam giác ADE cân tại A
=> ADE=AED(goác đáy tam giác cân)
mặt khác ABCD là hình thang cân => ADC=góc C
=> góc C= AED
mà 2 góc này ở vị trí đồng vị của AE và BC => AE//BC(2)
từ (1)và (2) => ABCE là hbh
b) xét tam giác AHE và tam giác FHD có góc AHE=góc DHF(đối đỉnh)
DH=HE(gt)
AE//DF(gt)=> AEH=FDH(SLT)
=>tam giác AHE=tam giác FHD(gcg) => AH=HF => H là TĐ của AF
c) Ta có AH=HF(câu b)DH=HE(gt) => ADFE là hbh
mà AH vg góc với ED=> AF vg góc với ED => ADEF là hình thoi
lại có tam giác ADE cân tại A (câu a)=> AD=AE => ADEF là hình vg

- Vì ABCD là hình bình hành nên ta có:
- AB // DC
- AB = DC
- Vì E là trung điểm của AB, ta có: \(A E = \frac{1}{2} A B\)
- Vì G là trung điểm của CD, ta có: \(D G = \frac{1}{2} D C\)
- Do AB = DC, nên \(\frac{1}{2} A B = \frac{1}{2} D C\).
- Suy ra, \(A E = D G\).
- Tứ giác có các cạnh đối song song.
- Tứ giác có các cạnh đối bằng nhau.
- Tứ giác có một cặp cạnh đối song song và bằng nhau.
- Ta đã có \(A E = D G\) (chứng minh ở câu a).
- Vì ABCD là hình bình hành nên AB // DC, suy ra AE // DG (vì E thuộc AB và G thuộc DC).
- Vì E là trung điểm của AB, ta có: \(A E = \frac{1}{2} A B\).
- Vì G là trung điểm của CD, ta có: \(C G = \frac{1}{2} C D\).
- Do ABCD là hình bình hành nên AB = CD.
- Từ đó suy ra, \(\frac{1}{2} A B = \frac{1}{2} C D\), tức là \(A E = C G\).
- Vì ABCD là hình bình hành nên AB // DC, suy ra AE // CG (vì E thuộc AB và G thuộc CD).
Ta giải lần lượt như sau:
Giả thiết: ABCD là hình bình hành, E là trung điểm AB, G là trung điểm CD.
a) Chứng minh \(A E = D G\)
- Vì E là trung điểm AB ⇒ \(A E = \frac{1}{2} A B\)
- G là trung điểm CD ⇒ \(D G = \frac{1}{2} C D\)
- Trong hình bình hành: \(A B = C D\)
⇒ \(A E = D G\) (đpcm).
b) Chứng minh tứ giác AEGD là hình bình hành
- \(A E \parallel D G\) vì \(A E\) cùng phương với AB, còn AB ∥ DC ⇒ AE ∥ DG.
- \(A E = D G\) (chứng minh ở câu a).
- Trong tứ giác, nếu một cặp cạnh đối song song và bằng nhau ⇒ tứ giác đó là hình bình hành.
⇒ AEGD là hình bình hành (đpcm).
c) Chứng minh tứ giác AECG là hình bình hành
- Xét AC và EG:
- Trong hình bình hành ABCD, AC và BD cắt nhau tại trung điểm O ⇒ O là trung điểm AC.
- E và G lần lượt là trung điểm AB, CD ⇒ EG nối trung điểm AB và CD ⇒ EG ∥ AC và EG = AC.
- Vậy AC ∥ EG và AC = EG ⇒ AECG là hình bình hành (đpcm).
Nếu bạn muốn mình có thể vẽ hình minh họa để nhìn rõ các điểm E và G, bạn sẽ thấy các quan hệ song song và bằng nhau rất trực quan.
Bạn có muốn mình vẽ không?

Mk vẽ hình trước bạn nhé ! Còn giải thì mk đang làm>>
o B A C D N F E M
a. Ta có: ^ABD = ^CDB ( so le trong ) => ^NBO = ^MDO
Xét \(\Delta\)NBO và \(\Delta\)MBO
có: ^NBO = ^MDO ( chứng minh trên )
OD = OB ( tính chất đường chéo hình bình hành)
^DOM = ^BON ( đối đỉnh )
=> \(\Delta\)NBO và \(\Delta\)MBO (1)
=> ON = OM
mà O nằm giữa M và N
=> M đối xứng vs N qua O
b. (1) => BN = DM và AB = DC => \(\frac{DM}{DC}=\frac{BN}{AB}\)(2)
Có: NF // AC => \(\frac{NF}{AC}=\frac{BN}{AB}\)(3)
ME//AC => \(\frac{ME}{AC}=\frac{DM}{DC}\)(4)
(2 ); (3) ; (4) => \(\frac{ME}{AC}=\frac{NF}{AC}\)
=> ME = NF mặt khác ME //NF ( //AC )
=> NFME là hình bình hành.

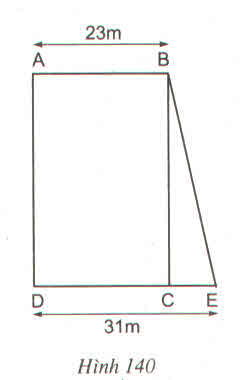
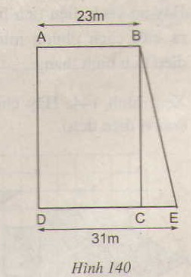
Ta có SABCD = AB. AD = 828 m2
Nêm AD = 8282382823 = 36 (m)
Do đó diện tích của hình thang ABED là:
SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2)
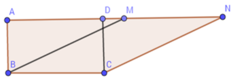
Vì ABCD là hình chữ nhật và BCNM là hình bình hành nên ta có:
SABCD = BC. DC
SBCNM = MN. DC
Mà BC = MN (do BCNM là hình bình hành nên SABCD = SBCNM
Lại có: theo giả thiết SABCD = 25 cm2 => SBCNM = 25 cm2
Đáp án cần chọn là: A