Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn tự vẽ hình nha
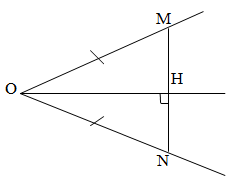
a) Xét tam giác OHM và tam giác OHN có:
ON=OM (vì tam giác OMN là tam giác cân )
OH chung
góc N= góc M (vì tam giác cân có 2 góc đáy bằng nhau)
suy ra tam giác OHN=tam giác OHM (c.g.c)
b) vì tam giác OMN là tam giác cân
mà OH là đường cao đông thời là đường phân giác
suy ra :OH là phân giác của góc MON

a) ta có OM = ON (gt)
=> OMN cân tại O
b) vì OMN cân tại O mà góc MON = 60 độ
-> góc OMN=góc ONM = (180 - 60 ) : 2 = 60 độ
=> tan giác OMN đều
xét Tam giác OHM và tam giác OHN
có OM = ON (gt)
góc ONH = góc OMH (OMN là tam giác cân)
góc ONH = góc OMH (H là đường cao )
=> tam giác OHM = tam giác OHN ( g-c-g)
=> HM = HN ( 2 cạnh tương ứng )

Kéo dài BO cắt Dy tại N
\(\Rightarrow\widehat{ABN}=\widehat{BNC}=60^o\) (góc so le trong)
Xét tg ONC có
\(\widehat{NOC}=180^o-\left(\widehat{BNC}+\widehat{OCN}\right)=180^o-\left(60^o+30^o\right)=90^o\Rightarrow OB\perp OC\)

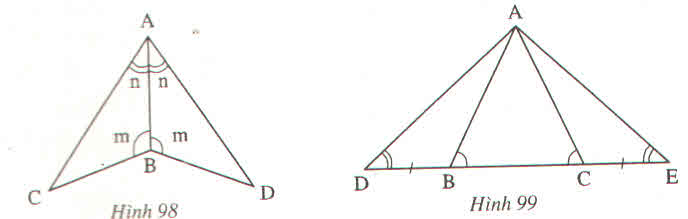
- Xem hình 98
∆ABC và ∆ABD có:
∠CAB = ∠DAB(gt)
AB là cạnh chung.
∠CBA = ∠DBA (gt)
Nên ∆ABC=∆ABD(g.c.g)
- Xem hình 99.
Ta có:
∠ABC + ∠ABD =1800 (Hai góc kề bù).
∠ACB + ∠ACE =1800
Mà ∠ABC = ∠ACB(gt)
Nên ∠ABD = ∠ACE
* ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
BD=EC(gt)
∠ADB = ∠AEC (gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
∠ADC = ∠AEB (gt)
∠ACD = ∠ABE (gt)
Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB
Nên ∆ADC=∆AEB(g.c.g)





 -0,75)
-0,75) =21/10
=21/10





a, Ta có:OM=ON\(\Rightarrow\Delta\)OMN cân tại O\(\Rightarrow\widehat{OMN}=\widehat{ONM}\)
Xét ΔOHM và ΔOHN có:
\(\widehat{OHN}=\widehat{OHM}\left(=90^o\right)\)
Chung OH
OM=ON(gt)
\(\Rightarrow\Delta OHM=\Delta OHN\left(ch-gn\right)\)
b, \(\Delta OHM=\Delta OHN\left(cma\right)\Rightarrow HM=HN\) (2 cạnh tương ứng)
a) Xét tam giác OHM vuông tại H và tam giác OHN vuông tại H ta có:
\(\widehat{H1}=\widehat{H2}\) \(\left(OH\perp MN\right)\)
OM = ON (kí hiệu giống nhau)
=> Tam giác OHM = tam giác OHN (ch-gn)
b) Ta có tam giác OHM = tam giác OHN => HM = HN (cạnh tương ứng)