Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ Az//Bx//Dy
=> BAD = BAz + DAz = (180o - ABx) + (180o - ADy) = 30o + 60o = 90o

Ta có hình vẽ:
A x B C y z 120 160
Vẽ tia Bz nằm trong góc ABC sao cho: Ax // Bz
Do Ax // Cy => Ax // Bz // Cy
Ta có:
- xAB + ABz = 180o (trong cùng phía)
=> 120o + ABz = 180o
=> ABz = 180o - 120o
=> ABz = 60o (1)
- zBC + BCy = 180o (trong cùng phía)
=> zBC + 160o = 180o
=> zBC = 180o - 160o
=> zBC = 20o (2)
Từ (1) và (2), lại có: ABz + zBC = ABC
=> 60o + 20o = ABC
=> ABC = 80o = B
Vậy góc B = 80o
vẽ đường thẳng a đi qua B và a // xA ; a //yC
=> xAB + ABa =180 độ (góc trong cùng phía)
=> ABa = 180 - 120 = 60 độ
aBC + yCB =180 độ (góc trong cùng phía)
=> góc aBC = 180 độ - 160 độ = 20 độ
Vì ABa +aBC = góc B
Thay số ta có :
60độ + 20 độ =80 độ
=> góc B =80 độ (đpcm)

Hình 1: ta có: \(\hat{NAI}=\hat{AID}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//DH
Ta có: \(\hat{AID}=\hat{AKM}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên DH//MK
Ta có: AN//DH
DH//MK
Do đó: AN//DH//MK
Hình 2:
Ta có: \(\hat{N}+\hat{H}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên MN//HK

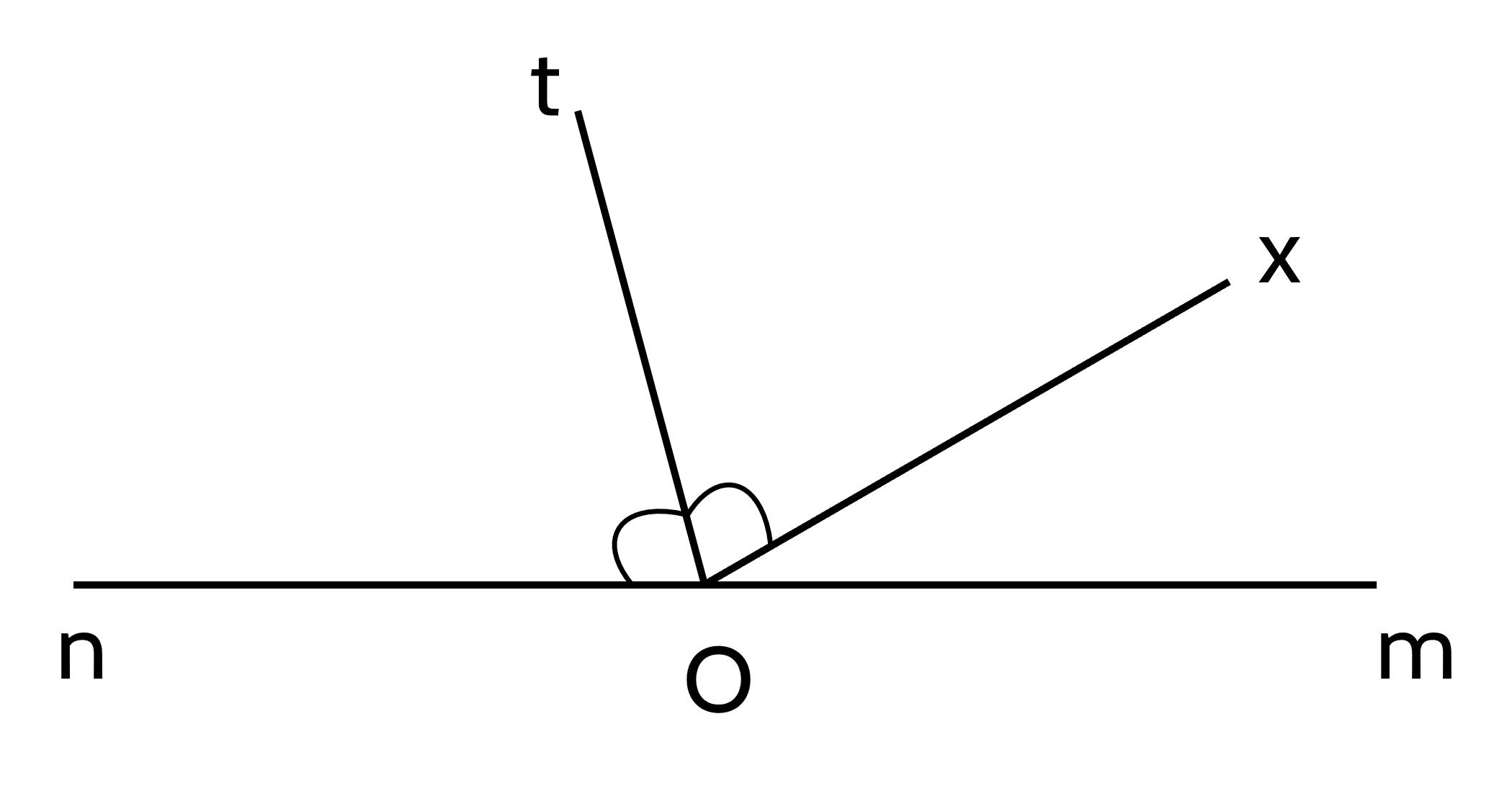
a) Ta có:
∠mOx + ∠nOx = 180⁰ (kề bù)
⇒ ∠nOx = 180⁰ - ∠mOx
= 180⁰ - 30⁰
= 150⁰
Do Ot là tia phân giác của ∠nOx
⇒ ∠nOt = ∠nOx : 2
= 150⁰ : 2
= 75⁰
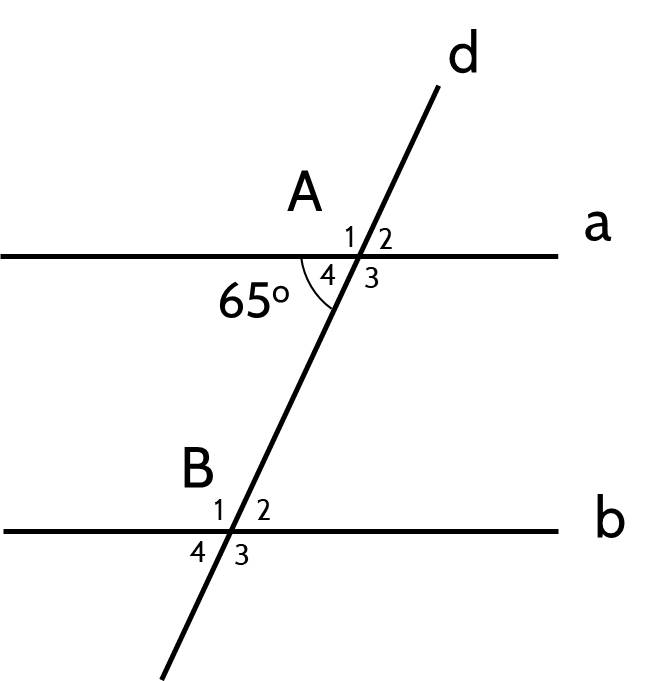
b) Do a // b
⇒ ∠B₄ = ∠A₄ = 65⁰ (đồng vị)
Ta có:
∠B₃ + ∠B₄ = 180⁰ (kề bù)
⇒ ∠B₃ = 180⁰ - ∠B₄
= 180⁰ - 65⁰
= 115⁰
Tính số đo góc �3^B3.
Hướng dẫn giải:a) ���^+���^=180∘mOx+xOn=180∘
Vậy ���^=180∘−30∘=150∘nOx=180∘−30∘=150∘.
��Ot là tia phân giác của ���^nOx, suy ra ���^=12.���^=75∘nOt=21.nOx=75∘.
b) a // b suy ra �4^=�2^=65∘A4=B2=65

Em thấy bạn Vuông nói đúng
Để chứng minh điều này, ta có thể chỉ ra trường hợp 2 góc bằng nhau nhưng không đối đỉnh.
Ví dụ:

\(\widehat {{O_1}} = \widehat {{O_2}}\) nhưng hai góc này không đối đỉnh

a: Ta có: \(\hat{A_2}+\hat{A_1}=180^0\) (hai góc kề bù)
=>\(\hat{A_2}=180^0-75^0=105^0\)
ta có: \(\hat{A_1}=\hat{A_3}\) (hai góc đối đỉnh)
mà \(\hat{A_1}=75^0\)
nên \(\hat{A_3}=75^0\)
Ta có: \(\hat{A_2}=\hat{A_4}\) (hai góc đối đỉnh)
mà \(\hat{A_2}=105^0\)
nên \(\hat{A_4}=105^0\)
Ta có: \(\hat{B_3}+\hat{B_4}=180^0\) (hai góc kề bù)
=>\(\hat{B_4}=180^0-120^0=60^0\)
ta có: \(\hat{B_3}=\hat{B_1}\) (hai góc đối đỉnh)
mà \(\hat{B_3}=120^0\)
nên \(\hat{B_1}=120^0\)
Ta có: \(\hat{B_4}=\hat{B_2}\) (hai góc đối đỉnh)
mà \(\hat{B_4}=60^0\)
nên \(\hat{B_2}=60^0\)
b: Ta có: \(\hat{xEF}=90^0\)
=>xx'⊥zz' tại E
=>\(\hat{xEz}=\hat{x^{\prime}Ez}=\hat{x^{\prime}EF}=90^0\)
Ta có: \(\hat{yFz^{\prime}}+\hat{y^{\prime}Fz^{\prime}}=180^0\) (hai góc kề bù)
=>\(\hat{yFz^{\prime}}=180^0-110^0=70^0\)
ta có: \(\hat{y^{\prime}Fz^{\prime}}=\hat{yFz}\) (hai góc đối đỉnh)
mà \(\hat{y^{\prime}Fz^{\prime}}=110^0\)
nên \(\hat{yFz}=110^0\)
Ta có: \(\hat{yFz^{\prime}}=\hat{y^{\prime}Fz}\) (hai góc đối đỉnh)
mà \(\hat{yFz^{\prime}}=70^0\)
nên \(\hat{y^{\prime}Fz}=70^0\)

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)

2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)








Lời giải:
Kẻ $Dt\parallel Ex\parallel Gy$ ($Dt$ nằm cùng phía với $Ex$ trên mặt phẳng bờ $DE$)
Vì $Dt\parallel Ex$ nên:
$\widehat{xED}+\widehat{EDt}=180^0$ (2 góc trong cùng phía)
$\Rightarrow \widehat{EDt}=180^0-\widehat{xED}=180^0-120^0=60^0$
Vì $Dt\parallel Gy$ nên $\widehat{tDG}=\widehat{DGy}=30^0$ (2 góc so le trong)
$\Rightarrow \widehat{EDG}=\widehat{EDt}+\widehat{tDG}=60^0+30^0=90^0$