K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CW
8 tháng 6 2016
A^ + B^ = 90o (phụ nhau)
A^ + 2* A^=90o
3* A^ = 90o
A^= 30o
B^= 2* A^ =2* 30o = 60o
a)
Xét \(\Delta\)ACD và \(\Delta\)ACB:
ACD^ = ACB^= 90o
AC chung
CD =CB
=> \(\Delta\)ACD =\(\Delta\)ACB (2 cạnh góc vuông)
=> AD = AB(2 cạnh tương ứng)
Phải là :Trên AD lấy M, trên AB lấy N (AM = AN) chứ.
b)
\(\Delta\)ACD =\(\Delta\)ACB (cmt) => A1 =A2 (2 góc tương ứng)
Xét \(\Delta\)AMC và \(\Delta\)ANC:
AC chung
A1 =A2 (cmt)
AM =AN
=> \(\Delta\)AMC = \(\Delta\)ANC (c.g.c)
=> CM =CN (2 cạnh tương ứng)
c)
AD = AB (cmt) =. D^ = B^
D^ + B^ + DAB^ =180o
2* D^ +DAB^=180o
D^= \(\frac{180o-DAB}{2}\) (1)
Ta có: AM = AN => AMN^ = ANM^
AMN^ + ANM^ + DAB^ =180o
2* AMN^ + DAB = 180o
AMN^ = \(\frac{180o-DAB}{2}\) (2)
Từ (1) và (2) => D^ = AMN^
Mà D^ so le trong với AMN^ => MN // DB
9 tháng 9 2021
Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(CN=ND=\dfrac{CD}{2}\)
mà AB=CD
nên AM=MB=CN=ND
C
1
29 tháng 4 2017
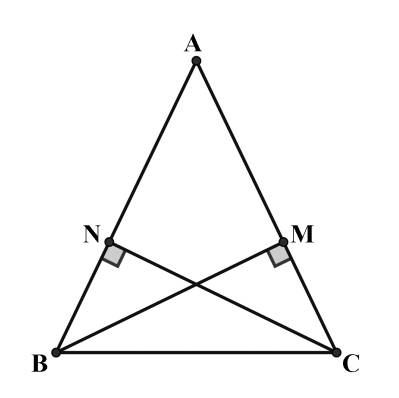
a/Xét tg ABE và tg CKE có:
EB=EK ( gt)
góc BEA=góc KEC(đối đỉnh)
AE=EC(BE trung tuyến AC =>E trung điểm AC)
=> Tg ABE=tg CKE( c.g.c)
b/ Xét tg AME ( vuông tại M) và tg CNE ( vuông tại N) có:
AE=EC(cmt)
góc BEA=góc KEC
=> Tg AME= tg CNE( ch-gn)
=> AM=CN ( hai cạnh tương ứng)
c/ Trong tg BCK có:
BC+CK > BK ( BĐT tg)
=> BC+CK > 2BE
Mà CK=AB( tg ABE=tg CKE)
=> AB+BC > 2BE
=> \(\frac{AB+BC}{2}>BE\)
d/ mk` ko giải được.
- Kẻ BD // AM ⇒ AM // BD // CN
- \(\Rightarrow\left\{{}\begin{matrix}\hat{MAB}=\hat{B}_{trên}\left(slt\right)\\\hat{NCB}=\hat{B}_{dưới}\left(slt\right)\end{matrix}\right.\)
- Cộng 2 vế ta được:
\(\hat{MAB}+\hat{NCB}=\hat{B}_{trên}+\hat{B}_{dưới}\)
hay: \(\hat{A}+\hat{C}=\hat{ABC}\left(đpcm\right)\)