Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔBAC có \(\cos ACB=\dfrac{CA^2+CB^2-AB^2}{2\cdot CA\cdot CB}\)
\(\Leftrightarrow3^2+5^2-AB^2=\dfrac{1}{2}\cdot2\cdot3\cdot5=15\)
\(\Leftrightarrow AB^2=19\)
hay \(AB=\sqrt{19}\left(cm\right)\)

\(cosCMB=\dfrac{BM^2+MC^2-BC^2}{2\cdot BM\cdot MC}\)
=>\(2^2-10^2+MC^2=2\cdot2\cdot MC\cdot cos135\)
=>\(MC^2+2\sqrt{2}\cdot MC-96=0\)
=>\(MC=6\sqrt{2}\left(cm\right)\)
góc AMC=180-135=45 độ
=>ΔAMC vuông cân tại A
=>\(AM=MC\cdot sin45=6\sqrt{2}\cdot\dfrac{1}{\sqrt{2}}=6\left(cm\right)\)
=>AC=6(cm)

\(\cos BCA=\dfrac{BC^2+AC^2-AB^2}{2\cdot AC\cdot BC}\)
\(\Leftrightarrow5^2+3^2-AB^2=2\cdot3\cdot5\cdot\dfrac{1}{2}=15\)
hay \(AB=\sqrt{19}\left(cm\right)\)

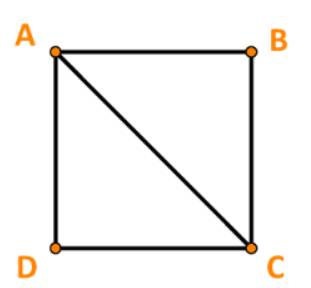
Ta có: \(|\overrightarrow {AB} | = AB\) và \(|\overrightarrow {AC} |\; = AC.\)
Mà \(AB = 3,\;AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{3^2} + {3^2}} = 3\sqrt 2 \)
\( \Rightarrow \;|\overrightarrow {AB} |\, = 3;\;\;|\overrightarrow {AC} |\, = 3\sqrt 2 \)

AM=2/3AB
=>BM=1/3AB
=>\(\dfrac{S_{BMC}}{S_{BAC}}=\dfrac{1}{3}\)
=>\(S_{BAC}=3\cdot S_{BMC}=12\sqrt{3}\)
\(\Leftrightarrow\dfrac{1}{2}\cdot AB\cdot AC\cdot sinBAC=12\sqrt{3}\)
=>\(\dfrac{1}{2}\cdot8\cdot AB\cdot sin120=12\sqrt{3}\)
=>\(AB\cdot2\sqrt{3}=12\sqrt{3}\)
=>AB=6

Không có hình nên không làm được nha b
phải có cả hình thì mới biết hình gì mà tính chứ bạn nhỉ ?