NL
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
LT
12 tháng 5 2017
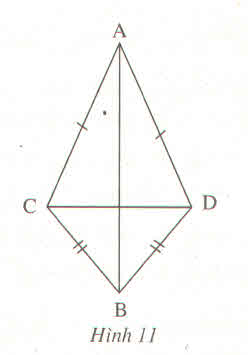
vì AC=AD=>A thuộc đường trung trực của CD
CB=BD=>B thuộc đường trung trực của CD
=>AB thuộc đường trung trực của CD=>AB vuông góc với CD
QD
20 tháng 4 2017
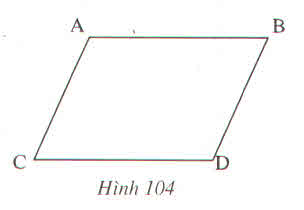
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
ˆA1A1^= ˆD1D1^(so le trong AB//CD)
AD là cạnh chung.
A2^=D2^(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
Xem thêm tại: http://loigiaihay.com/bai-38-trang-124-sach-giao-khoa-toan-7-tap-1-c42a5073.html#ixzz4elm8F0eT
6 tháng 8 2017
A B C D
Vẽ đoạn thẳng AD.
∆ADB và ∆DAC có:
\(\widehat{A^1}\)= \(\widehat{D^1}\)(so le trong AB//CD)
AD là cạnh chung.
\(\widehat{A^2}\)=\(\widehat{D^2}\)(So le trong, AC//BD)
Do đó ∆ADB=∆DAC(g.c .g)
Suy ra: AB=CD, BD=AC
2 tháng 6 2017
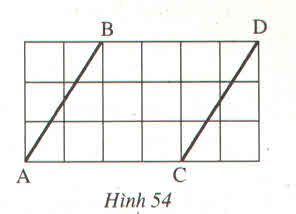
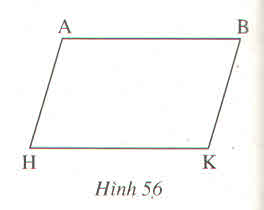
Nối A với K
Xét tam giác ABK và tam giác AHK có:
AK: cạnh chung
góc BAK = góc AKH (AB // HK)
góc HAK = góc AKB (AH //BK)
=> tam giác ABK = tam giác AHK
=> AB = HK (hai cạnh tương ứng)
Ta có: tam giác ABK = tam giác AHK
=> AH = BK (hai cạnh tương ứng)
DT
1 tháng 12 2017
kẻ đoạn thẳng AK
Xét tamgiác KAH và tam giác AKB
góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )
cạnh AK chung
góc HKA = góc BAK (2 góc so le trong do AB //HK )
=> tam giác KAH = tam giác AKB ( g.c.g.)
=> AB=HK (2 cạnh tương ướng )
=> AH = BK (2 cạnh tương ướng )
đúng không..............................................
SG
1
4 tháng 4 2019
Xét /\\(\) AMI:MA<MI+IA
Cộng MB vào hai vế :
MA+MB<MI+IA+MB
=>MA+MB<IB+IA (1)
Xét /\ BIC:IB<IC+CB
Cộng IA vào hai vế:
IB+IA<IC+CB+IA
=>IB+IA<CA+CB (2)
Từ (1),(2) ta có MA+MB<IA+IB<CA + CB
SG
1
HQ
13 tháng 4 2018
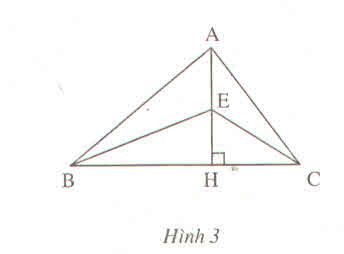
Ta có: AB > AC (gt)
Suy ra: HB > HC (đường xiên lớn hơn có hình chiếu lớn hơn)
Suy ra: EB > EC (hình chiếu lớn hơn thì có đường xiên lớn hơn)
SG
3
13 tháng 5 2017
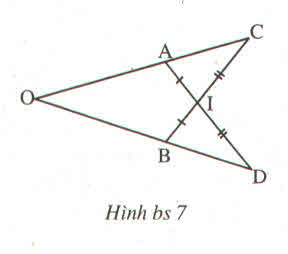
Xét tam giác IAC và IBD có:
IA = IB ( theo đề bài)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( theo đề bài )
Do đó: tam giác IAC = tam giác IBD (c.g.c)
Suy ra góc ACI = góc BDI ( 2 góc tương ứng) \(\left(1\right)\)
Suy ra góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = \(180^0\)(2 góc kề bù)
góc OBI + góc IBD = \(180^0\)(2 góc kề bù)
mà: góc IAC = góc IBD (*)
Suy ra góc: OAI = góc OBI (5)
Xét tam giác: OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
Do đó: tam giác OAD = tam giác OBC (g.c.g)
Suy ra: OA = OB (2 cạnh tương ứng)
20 tháng 1 2019
Xét tam giác IAC và tam giác IBD có:
IA = IB ( gt)
Góc AIC = góc BID ( 2 góc đối đỉnh)
IC = ID ( gt )
=> Tam giác IAC = tam giác IBD (c.g.c)
=> Góc ACI = góc BDI ( 2 góc tương ứng) (1)
và góc IAC = IBD ( 2góc tương ứng) (*)
Có I nằm giữa B và C
Suy ra: BI + CI = BC (2)
Có I nằm giữa A và D
Suy ra: AI + DI = AD (3)
Từ 2 và 3 suy ra: BC = AD (4)
Có góc OAI + góc IAC = 1800 (2 góc kề bù)
góc OBI + góc IBD = 1800 (2 góc kề bù)
mà: góc IAC = góc IBD (*)
=> góc: OAI = góc OBI (5)
Xét tam giác OAD và tam giác OBC có:
góc ACI = góc BDI (1)
AD = BC (4)
góc OAI = góc OBI (5)
=> Tam giác OAD = tam giác OBC (g.c.g)
=> OA = OB (2 cạnh tương ứng)
SG
3
LD
12 tháng 3 2018
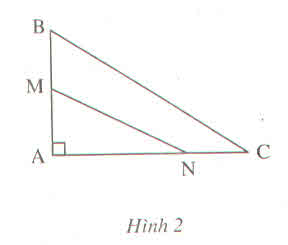
Hình chiếu của AN < hình chiếu của AC
=> đường xiên BN < đường xiên của BC (1)
Hình chiếu của AM < hình chiếu AB => đường xiên MN < đường xiên NB. (2)
Từ (1) và (2) suy ra:
MN< BN< BC.
SG
2
VM
29 tháng 12 2019
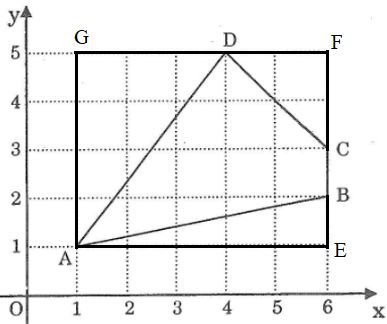
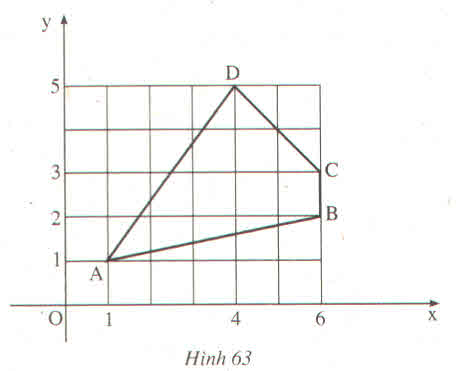
Ta có: \(BC=1.\)
+ Xét \(\Delta ABE\) vuông tại E có:
\(AB^2=AE^2+BE^2\) (định lí Py - ta - go).
=> \(AB^2=5^2+1^2\)
=> \(AB^2=25+1\)
=> \(AB^2=26\)
=> \(AB=\sqrt{26}\) (vì \(AB>0\)).
+ Xét \(\Delta CDF\) vuông tại F có:
\(CD^2=DF^2+CF^2\) (định lí Py - ta - go).
=> \(CD^2=2^2+2^2\)
=> \(CD^2=4+4\)
=> \(CD^2=8\)
=> \(CD=\sqrt{8}\) (vì \(CD>0\)).
+ Xét \(\Delta ADG\) vuông tại G có:
\(AD^2=AG^2+DG^2\) (định lí Py - ta - go).
=> \(AD^2=4^2+3^2\)
=> \(AD^2=16+9\)
=> \(AD^2=25\)
=> \(AD=5\) (vì \(AD>0\)).
Vậy \(AB=\sqrt{26};BC=1;CD=\sqrt{8};AD=5.\)
Chúc bạn học tốt!
MH
26 tháng 5 2017
Ta tính được : AB = \(\sqrt{26}\) ; CD = \(\sqrt{8}\) ; BC = 1 ; DA = 5
Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(CN=ND=\dfrac{CD}{2}\)
mà AB=CD
nên AM=MB=CN=ND