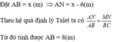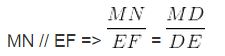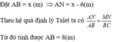
Biết MN = 1,5cm, BC = 6m, BN =...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. a, ∠ANM = ∠CBN (=90 độ) (chúng ở vị trí đồng vị) => MN//BC , theo hệ quả định lý Talet ta có: AN/AB = MN/BC, cho AB=x (cm) thì AN = x-6 (cm) Nên: (x-6)/x=1,5/6 => x=8(cm) Nên AB = 8 cm b, AD là đường phân giác của tam giác ABC nên: AB/AC = BD/DC, nếu cho BD=x (cm) thì ta có DC=5-x (cm) Nên: 4/6=x/(5-x) => 20=10x => x=2 (cm), nên BD= 2 cm => DC=3 cm Theo hình vẽ ta có: AC//BE => ∠ACD = ∠DBE (so le trong) Xét △BDE và △CDA có: ∠ACD=∠DBE (c/m tr) ∠ADC=∠BDE (đối đỉnh) => △BDE=△CDA (g.g) => BE/AC = BD/CD => BE/6=2/3 => BE=12:3=4 (cm) Vậy: BD= 2 cm BE= 4 cm * Trong hình 14a mà DE = MD + ME = 9.5 + 28 = 37.5 * Trong hình 14b Ta có A’B’ ⊥ AA'(gt) và AB ⊥ AA'(gt) => A’B’ // AB => ∆ABO vuông tại A => OB2 = y2 = OA2 + AB2 => y2 = 62+ 8,42 => y2 = 106,56 => y ≈ 10,3 Ta có SABCD = AB. AD = 828 m2 Nêm AD = 8282382823 = 36 (m) Do đó diện tích của hình thang ABED là: SABED= (AB+DE).AD2(AB+DE).AD2 = (23+31).362(23+31).362 = 972(m2) ) Những cạnh song song với cạnh CC1 là: AA1, BB1, DD1 b) Những cạnh song song với cạnh A1D1 là: B1C1, BC, AD