Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2:
a) Ta có : Từ \(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Rightarrow\dfrac{5a}{5c}=\dfrac{7b}{7d}\)
Theo tính chất dãy tỉ số bằng nhau, ta có :
\(\dfrac{5a}{5c}=\dfrac{7b}{7d}=\dfrac{5a+7b}{5c+7d}\left(1\right)\)
Và \(\dfrac{5a}{5c}=\dfrac{7b}{7d}=\dfrac{5a-7b}{5c-7d}\left(2\right)\)
Từ (1) và (2)=> \(\dfrac{5a+7b}{5c+7d}=\dfrac{5a-7b}{5c-7d}\Rightarrow\dfrac{5a+7b}{5a-7b}=\dfrac{5c+7d}{5c-7d}\)Vậy...
b) Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Thay các đẳng thức vừa tìm được , ta có :
\(\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=k^2\left(1\right)\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}\)
\(=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
từ (1) và (2)=> đpcm
tik mik nha !!!
1. Bạn xem lại đề bài nhé! Mình nghĩ là \(2x=3y=5z\) thì đúng hơn!
2.
a) Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Rightarrow\dfrac{5a}{5c}=\dfrac{7b}{7d}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{5a}{5c}=\dfrac{7b}{7d}=\dfrac{5a+7b}{5c+7d}=\dfrac{5a-7b}{5c-7d}\)
Từ \(\dfrac{5a+7b}{5c+7d}=\dfrac{5a-7b}{5c-7d}\Rightarrow\dfrac{5a+7b}{5a-7b}=\dfrac{5c+7d}{5c-7d}\)(đpcm)
Vậy \(\dfrac{5a+7b}{5a-7b}=\dfrac{5c+7d}{5c-7d}\)
b) Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
\(\Rightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có:
\(VT=\dfrac{ac}{bd}=\dfrac{bk.dk}{bd}=\dfrac{bd.k^2}{bd}=k^2\left(1\right)\)
\(VP=\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{b^2.k^2+d^2.k^2}{b^2+d^2}=\dfrac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\left(đpcm\right)\)
Vậy \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
1. đề bạn ghi rõ lại giúp mình đc ko r mình giải lại cho
2. Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{2x^2}{2.3^2}=\dfrac{y^2}{5^2}=\dfrac{2x^2-y^2}{18-25}=\dfrac{-28}{-7}=4\)
\(\dfrac{x}{3}=4\Rightarrow x=12\)
\(\dfrac{y}{5}=4\Rightarrow y=20\)
Vậy x=12 và y=20
a) Có : \(\widehat{BON}=\widehat{BOM}+\widehat{MON}=90^0+\widehat{MON}\)
Và : \(\widehat{AOM}=\widehat{AON}+\widehat{MON}=90^0+\widehat{MON}\)
=> \(\widehat{BOM}=\widehat{AON}\)
b) Có : \(\widehat{BON}+\widehat{AOM}=\widehat{BOM}+2\widehat{MON}+\widehat{AON}=180^0\)
Mặt khác : \(\widehat{BOM}+\widehat{MON}+\widehat{AON}=150^0\)
=> \(\widehat{MON}=180^0-150^0=30^0\)
bài 1 : a) oh là tia đối oz \(\Rightarrow\) zoh thẳng hàng
ot là tia đối của tia ox \(\Rightarrow\) xot thẳng hàng
ta có : xoz = \(\dfrac{100}{2}=50^0\) (oz là tia phân giác của góc xoy)
mà xoz = toh (đối đỉnh) \(\Rightarrow\) toh = 500
b) ta có : toh = xoz (đối đỉnh)
mà toh = 400 \(\Rightarrow\) xoz = 400
\(\Rightarrow\) xoy = 40.2 = 800
bạn ơi tớ bảo phần ab bài 1 tớ biết làm rồi tớ muốn cậu có thể giúp tớ bài 2 và bài 3,bài 1 c,d được không
xin cảm ơn các bạn trước!
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{y+x+t}=\dfrac{y}{z+t+x}=\dfrac{y}{t+x+y}=\dfrac{t}{x+y+z}=\dfrac{x+y+z+t}{3\left(x+y+z+t\right)}=\dfrac{1}{3}\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+z=3t\\y+z+t=3x\\z+t+x=3y\\t+x+y=3z\end{matrix}\right.\)
\(\Rightarrow x=y=z=t\)
Thay vào P ta được :
\(P=1+1+1+1=4\)
Với mọi x thuộc R Có (x^2-9)^2 \(\ge\) 0
[y-4] \(\ge\) 0
Suy ra (x^2-9)^2+[y-4] - 1 \(\ge\) -1
Xét A=-1 khi và chỉ khi (x^2-9)^2 và [y-4] đều bằng 0
Tự tính ra
Xin lỗi nhưng vì không biết nên mình phải dùng [ ] thay cho GTTĐ nhé
Xin lỗi nhiều tại mình o tìm được kí hiệu đó
,ngày mai tớ đi hok rùi
.huhu
.mấy anh chị CTV hok giỏi thì giúp em vs
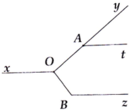
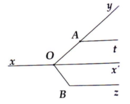
=> y O x ' ^ = y A t ^ (hai góc đồng vị bằng nhau)
=> Ox' // At (1).
Mặt khác: OA ⊥ OB => A O B ^ = 90 °
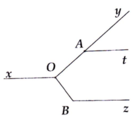
=> x ' O B ^ = y O B ^ − y O x ' ^ = 90 ° − 40 ° = 50 °
=> x ' O B ^ = O B z ^ = 50 ° + 130 ° = 180 °
(hai góc trong cùng phía bù nhau)
=>Ox' //Bz (2).
Từ (1) và (2), suy ra At //Bz