TD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
27 tháng 7 2023
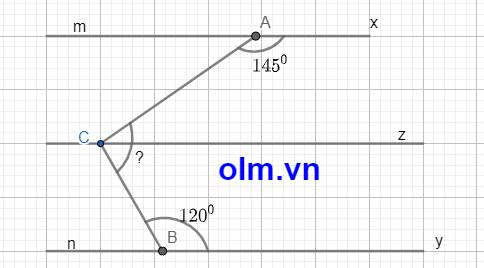
Ta có: \(\widehat{ACz}\) và \(\widehat{CAx}\) là hai góc trong cùng phía nên:
\(\widehat{ACz}\) + \(\widehat{CAx}\) = 1800 ⇒ \(\widehat{ACz}\) = 1800 - 1450 = 350
Mặt khác ta cũng có: \(\widehat{BCz}\) và \(\widehat{CBy}\) là hai góc trong cùng phía nên:
\(\widehat{BCz}\) + \(\widehat{CBy}\) = 1800 ⇒ \(\widehat{BCz}\) = 1800 - 1200 = 600
\(\widehat{ACB}\) = \(\widehat{ACz}\) + \(\widehat{BCz}\) = 350 + 600 = 950
Kết luận: \(\widehat{ACB}\) = 950
AH
Akai Haruma
Giáo viên
21 tháng 8 2023
Lời giải:
Ta thấy:
$\widehat{yBA}+\widehat{BAx}=124^0+56^0=180^0$. Mà 2 góc này ở vị trí trong cùng phía nên $By\parallel Ax$ (đpcm)
5 tháng 10 2021
\(a,Ax//By\Rightarrow\widehat{ABy}=\widehat{BAx}=120^0\left(so.le.trong\right)\\ b,\widehat{ABy}=\widehat{BCz}\left(=120^0\right)\)
Mà 2 góc này ở vị trí đồng vị nên \(By//Cz\)
Mà \(By//Ax\) nên \(Cz//Ax\)
Vậy có 3 cặp tia song song là \(Ax//By;By//Cz;Cz//Ax\)
14 tháng 10 2023
Kẻ Cz//Ax
Cz//Ax
Ax//By
Do đó: Cz//By
Cz//Ax
=>\(\widehat{zCA}+\widehat{xAC}=180^0\)(hai góc trong cùng phía)
Cz//By
=>\(\widehat{zCB}+\widehat{yBC}=180^0\)(hai góc trong cùng phía)
\(\widehat{xAC}+\widehat{ACB}+\widehat{CBy}\)
\(=\widehat{zCA}+\widehat{xAC}+\widehat{zCB}+\widehat{yBC}\)
=180+180
=360 độ
MT
22 tháng 6 2015
kẻ tia Ot // Ax mà Ax//By
nên Qt//Ax//By
Ay//Ot
=>g xAO + g AOt=1800 ( hai góc trong cùng phía)
1050+ g AOt=1800
=>g AOt=1800-1050
=750
ta lại có gAOB=gAOt+gBOt
800=750+gBOt
=>gBOt=800-750=50
ta có Ot//By
=>gBOt+gOBy=1800(trong cùng phía)
50+gOBy=1800
=>gOBy=1800-50=1750
PN
0