Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:

Gọi O là giao điểm của AC và BD.
a) Áp dụng công thức \(S = \frac{1}{2}ac.\sin B\), ta có:
\(\begin{array}{l}{S_{OAD}} = \frac{1}{2}.OA.OD.\sin \alpha ;\quad {S_{OBC}} = \frac{1}{2}.OB.OC.\sin \alpha ;\\{S_{OAB}} = \frac{1}{2}.OA.OB.\sin ({180^o} - \alpha );\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin ({180^o} - \alpha ).\end{array}\)
Mà \(\sin ({180^o} - \alpha ) = \sin \alpha \)
\( \Rightarrow {S_{OAB}} = \frac{1}{2}.OA.OB.\sin \alpha ;\quad {S_{OCD}} = \frac{1}{2}.OD.OC.\sin \alpha .\)
\(\begin{array}{l} \Rightarrow {S_{ABCD}} = \left( {{S_{OAD}} + {S_{OAB}}} \right) + \left( {{S_{OBC}} + {S_{OCD}}} \right)\\ = \frac{1}{2}.OA.\sin \alpha .(OD + OB) + \frac{1}{2}.OC.\sin \alpha .(OB + OD)\\ = \frac{1}{2}.OA.\sin \alpha .BD + \frac{1}{2}.OC.\sin \alpha .BD\\ = \frac{1}{2}.BD.\sin \alpha .(OA + OC)\\ = \frac{1}{2}.AC.BD.\sin \alpha = \frac{1}{2}.x.y.\sin \alpha .\end{array}\)
b) Nếu \(AC \bot BD\) thì \(\alpha = {90^o} \Rightarrow \sin \alpha = 1.\)
\( \Rightarrow {S_{ABCD}} = \frac{1}{2}.x.y.1 = \frac{1}{2}.x.y.\)

A B C D P M
a) \(\overrightarrow{MP}.\overrightarrow{BC}=\dfrac{1}{2}\left(\overrightarrow{MA}+\overrightarrow{MD}\right).\left(\overrightarrow{BM}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}+\overrightarrow{MD}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MB}.\overrightarrow{MD}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{MA}.\overrightarrow{BM}+\overrightarrow{MD}.\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\left(0+0\right)=0\) (vì \(AC\perp BD\) nên \(\overrightarrow{MA}.\overrightarrow{BM}=0;\overrightarrow{MD}.\overrightarrow{MC}=0\)).
Vậy \(\overrightarrow{MP}.\overrightarrow{BC}=0\) nên \(MP\perp BC\).

Chọn D.
Ta có: AB2 + CD2 - BC2 - AD2
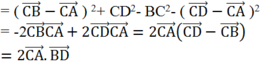
Do 2 đường chéo AC và BD vuông góc với nhau nên ![]()
Từ đó; AB2 + CD2 - BC2 - AD2 = 0 hay AB2 + CD2 = BC2 + AD2

M là trung điểm AB \(\Rightarrow\overrightarrow{IM}=\dfrac{1}{2}\left(\overrightarrow{IA}+\overrightarrow{IB}\right)\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=\left(\overrightarrow{IA}+\overrightarrow{IB}\right).\left(\overrightarrow{DI}+\overrightarrow{IC}\right)=\overrightarrow{IA}.\overrightarrow{DI}+\overrightarrow{IB}.\overrightarrow{IC}+\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}\)
\(=\overrightarrow{IA}.\overrightarrow{IC}+\overrightarrow{IB}.\overrightarrow{DI}=-IA.IC+IB.DI\)
Mặt khác do 2 tam giác vuông DIC và AIB đồng dạng (\(\widehat{IAB}=\widehat{IDC}\) cùng chắn BC)
\(\Rightarrow\dfrac{IA}{ID}=\dfrac{IB}{IC}\Rightarrow IA.IC=IB.ID\Rightarrow-IA.IC+IB.ID=0\)
\(\Rightarrow2\overrightarrow{IM}.\overrightarrow{DC}=0\Rightarrow IM\perp DC\)

A B C D I J
Áp dụng tính chất trung điểm ta có:
Do J là trung điểm của BD nên \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}\).
Theo quy tắc ba điểm: \(\overrightarrow{IB}=\overrightarrow{IA}+\overrightarrow{AB}\)
\(\overrightarrow{ID}=\overrightarrow{IC}+\overrightarrow{CD}\).
Vì vậy: \(2\overrightarrow{IJ}=\overrightarrow{IB}+\overrightarrow{ID}=\overrightarrow{IA}+\overrightarrow{AB}+\overrightarrow{IC}+\overrightarrow{CD}\)
\(=\left(\overrightarrow{IA}+\overrightarrow{IC}\right)+\left(\overrightarrow{AB}+\overrightarrow{CD}\right)\)
\(=\overrightarrow{AB}+\overrightarrow{CD}\) (ĐPCM).