Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
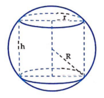
Gọi bán kính đáy và chiều cao của hình trụ lần lượt là r và h. Khi đó thiết diện qua trục của hình trụ là một hình chữ nhật có kích thước hai cạnh là 2r và h. Diện tích hình chữ nhật đó là S = 2 r h .
Quan sát hình vẽ, ta thấy R 2 = h 2 2 + r 2 ⇔ h = 2 R 2 − r 2 = 2 3 a 2 − r 2 .
Khi đó S = 2 r h = 4 r 3 a 2 − r 2 ≤ 4. r 2 + 3 a 2 − r 2 2 2 = 6 a 2 . Dấu “=” xảy ra khi và chỉ khi
r = 3 a 2 − r 2 ⇔ 2 r 2 = 3 a 2 ⇔ r = a 6 2 ⇒ h = 2 3 a 2 − 3 a 2 2 = a 6
Vậy diện tích toàn phần của hình trụ (T) là
S t p = 2 π r h + 2 π r 2 = 2 π a 6 . a 6 2 + 2 π a 6 2 2 = 9 π a 2 (đvdt).

Chọn A
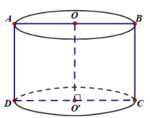
* Theo hình vẽ, do ABCD là hình vuông cạnh a nên ta có:


Bài giải
Ta có sơ đồ :
CDHHCN : I-----I-----I-----I-24,2-I
CRHHCN : I-----I-----I-----I
Hiệu số phần bằng nhau là :
5 - 3 = 2 ( phần )
Chiều rộng là : ( 24,2 : 2 ) x 3 = 36,3 ( cm )
Chiều dài là : 36,3 + 24,2 = 60,5 ( cm )
Chiều cao là : 36,3 : 2 = 18,15 ( cm )
Diện tích xung quanh là : ( 36,3 + 60,5 ) x 2 x 18,15 = 3513,84 ( cm2)
Diện tích toàn phần là : 3513,84 + 36,3 x 30,25 x 2 = 214783,47 ( cm2)
Thể tích là : 36,3 x 60,5 x 18,15 = 39860,1225 (cm3)
DS :...
Ta có sơ đồ :
CDHHCN : I-----I-----I-----I-24,2-I
CRHHCN : I-----I-----I-----I
Hiệu số phần bằng nhau là :
5 - 3 = 2 ( phần )
Chiều rộng là : ( 24,2 : 2 ) x 3 = 36,3 ( cm )
Chiều dài là : 36,3 + 24,2 = 60,5 ( cm )
Chiều cao là : 36,3 : 2 = 18,15 ( cm )
Diện tích xung quanh là : ( 36,3 + 60,5 ) x 2 x 18,15 = 3513,84 ( cm2)
Diện tích toàn phần là : 3513,84 + 36,3 x 30,25 x 2 = 214783,47 ( cm2)
Thể tích là : 36,3 x 60,5 x 18,15 = 39860,1225 (cm3)
DS :...

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2
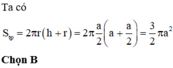


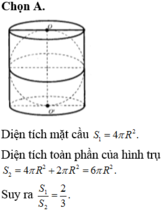

Đáp án là B