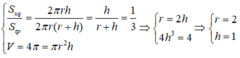Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
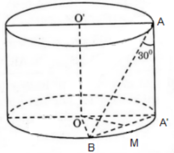
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

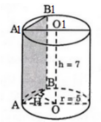
Do khoảng cách hai đáy là nên chiều cao của hình trụ (đồng thời là độ dài đường sinh) là h = l = 7.
Diện tích xung quanh của hình trụ là:
Sxq = 2π.r.l = 2π.5.7 = 70π ( c m 2 ).
Thể tích của khối trụ được tạo nên là:
V = π r 2 .h = π. 5 2 .7 = 175π ( c m 3 )

\(S_đ=\pi R^2\Rightarrow R=\dfrac{3}{\sqrt{\pi}}\left(cm\right)\)
\(S_{xq}=2\pi Rh=2\pi.\dfrac{3}{\sqrt{\pi}}.9=54\sqrt{\pi}\left(cm^2\right)\)
\(S_{tp}=2S_đ+S_{xq}=36+54\sqrt[]{\pi}\)
\(V=h.S_đ=9.18=162\left(cm^3\right)\)