Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
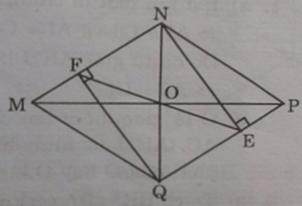
a) Ta có NF // QE (MNPQ là hình bình hành) (1)
NE ⊥ PQ; QF ⊥ MN
Mà MN // QP
⇒ NE // QF (2)
Từ (1) và (2) ⇒ tứ giác NEQF là hình bình hành có một góc vuông nên là hình chữ nhật.
b) O là giao điểm hai đường chéo hình thoi MNPQ nên O là trung điểm NQ.
Lại có NEQF là hình chữ nhật (cmt) nên đường chéo EF phải qua trung điểm O của NQ. Vậy MP, NQ, EF đồng quy tại O.

E là TĐ của MQ, F là TĐ của NP
=> EF là đ trung bình của hình thang MNPQ
=> EF//MN
hay ED//MN
mà E là TĐ của MQ
=> D là TĐ của QN
=> ED là đ trung bình của Δ MQN
=> ED=1/2MN(1)
Tương tự: BF=1/2MN(2)
Từ 1 và 2 => ED=BF
=> ED + DB=BF+DB => EB=FD
b,do EF là đ trung bình của hình thang MNPQ
=>\(EF=\dfrac{MN+PQ}{2}\)= \(\dfrac{3+5}{2}\)=4(cm) (3)
Do ED=BF=1/2MN
=> ED=BF=\(\dfrac{3}{2}\)(cm) (4)
Từ 3 và 4 => BD= EF-ED-BF=1(cm)

M N P Q I K 1 2 3 4
a) Vì MNPQ là hình thoi (gt)
MP cắt QN tại I (gt)
=> I trung điểm QN và MP (t/c hthoi)
Ta có: QP = PK (gt), P \(\in\) QK (gt)
=> P trung điểm QK (ĐN trung điểm)
Xét \(\Delta\)QNK có: I, P trung điểm QN, QK (cmt)
=> IP là đường trung bình \(\Delta\)QNK (ĐN đường TB \(\Delta\))
=> IP // NK (t/c đường TB \(\Delta\))
b) Vì MNPQ là hình thoi (gt)
=> MP \(\perp\) QN (t/c hthoi)
=> \(\widehat{I_1}=\widehat{I_2}=\widehat{I_3}=\widehat{I_4}=90^o\) (ĐN 2 đường thẳng \(\perp\))
mà IP // NK (cmt)
=> \(\widehat{QNK}=\widehat{I_4}=90^o\) (2 góc đồng vị)
Ta có: MI = IP (I trung điểm MP)
IP = \(\dfrac{1}{2}\)NK (IP là đường trung bình \(\Delta\)QNK)
=> \(\dfrac{MI}{NK}=\dfrac{1}{2}\)
mà I trung điểm QN (cmt)
=> \(\dfrac{QI}{QN}=\dfrac{1}{2}\) (t/c trung điểm)
do đó: \(\dfrac{MI}{MK}=\dfrac{QI}{QN}\)
Xét \(\Delta\)MQI và \(\Delta\)KQN có:
\(\widehat{I_1}=\widehat{QNK}\left(=90^o\right)\)
\(\dfrac{MI}{MK}=\dfrac{QI}{QN}\) (cmt)
=> \(\Delta\)MQI ~ \(\Delta\)KQN (c.g.c)
b) O là giao điểm hai đường chéo hình thoi MNPQ nên O là trung điểm NQ.
Lại có NEQF là hình chữ nhật (cmt) nên đường chéo EF phải qua trung điểm O của NQ. Vậy MP, NQ, EF đồng quy tại O.