Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.

1: Xét ΔACE có
I là trung điểm của AE
O là trung điểm của AC
Do đó: IO là đường trung bình của ΔACE
Suy ra: IO//CE
hay OIEC là hình thang

Giải thích các bước giải:
ta có: Tam giác ABC vuông tại A (gt)
=> AB^2+AC^2=BC^2
6^2+8^2 =BC^2
36+64 =BC^2
100 =BC^2
=>BC=10cm
Tam giác ABC vuông tại A có Am là đg trung tuyến
=> AM=BC/2=10/2=5cm
HÌNH VẼ THÌ BẠN TỰ VẼ NHÉ, HÌNH NÀY DỄ VẼ MÀ NHỈ.
Câu a bạn V (Team BTS) làm rồi nên mình chỉ làm các câu còn lại thôi nhé.
b) Vì DM vuông góc AB, AC vuông góc AB (gt) => DM // AC.
=> DMCA là hình thang mà góc ADM = góc DAC = 90 độ.
Do đó ADMC là hình thang vuông.
c) Xét tam giác ABC ta có: DM // AC (cmt), M là trung điểm BC (AM là trung tuyến)
=> D là trung điểm của AB.
Tứ giác AEBM có AB và EM là hai đường chéo cắt nhau tại trung điểm D. => AEBM là hình bình hành. (1)
Lại xét tam giác AMB cân tại M (MA=MB) có MD là trung tuyến => MD cũng là đường cao=> ME vuông góc AB tại D. (2)
Từ (1) và (2) => AEBM là hình thoi.
d) Vì AEBM là hình thoi => AE // BM, AE = BM.
Mà BM = MC => AE // MC, AE = MC. Do đó AEMC là hình bình hành.
e, Câu e mình không hiểu lắm vì thấy đề bài cứ sai sai làm sao. Mình chỉ chứng minh câu F đối xứng với E qua A thôi nhé.
Gọi I là giao điểm của AC và MF. Vì M đối xứng F qua AC => I là trung điểm MF, AC vuông góc MF tại I.
Chứng minh tương tự câu c ta sẽ được AFMC là hình thoi => AF // MC, AF = MC.
Mà AE // MC, AE = MC (cmt)
=> A, E, F thẳng hàng (tiên đề Ơ-clit) và A là trung điểm của EF (AE=AF)
Vậy F đối xứng E qua A.
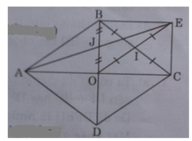
a) Ta có IB = IC (gt), IO = IE (tính chất đối xứng)
⇒ OBEC là hình bình hành.
Lại có ∠BOC = 90o (tính chất hai đường chéo hình thoi).
Do đó OBEC là hình chữ nhật.
b)Ta có OA = OC (tính chất đường chéo hình thoi)
Mà OC = BE và OC // BE (cmt) nên OA = BE và OA // BE.
Do đó ABEO là hình bình hành
Ta có J là trung điểm của OB nên đường chéo thứ hai AI phải qua J và JA = JE.
⇒ E đối xứng với A qua trung điểm J của đoạn OB.
A B C D O E I J
a, Xét tứ giác OBEC,
I là trung điểm BC, OI= IE
=> OBEC là hình bình hành
mà \(\widehat{BOC}=90^0\) ( Vì ABCD là hình thoi)
=> OBEC là hình chữ nhật
b,OBEC là hình chữ nhật => BE =OC ; BE//OC
mà OC =AO
=> BE = AO , BE//AO
=> ABEO là hình bình hành
=> Hai đg chéo cắt nhau tại trung điểm mỗi đươngf
mà J là trung điểm OB => J là trung điểm AE
=> E đối xứng A qua J