Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

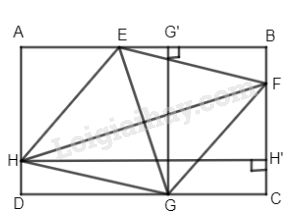
Gọi H′H′ là hình chiếu của H trên BC và G′G′ là hình chiếu của G trên AB.
Ta có: SEFGH=1/2EG.HFSEFGH=1/2EG.HF
Và SABCD=AD.CD;SABCD=AD.CD;
EG≥GG′=AD;EG≥GG′=AD;
HF≥HH′=CD.HF≥HH′=CD.
Do đó: SEFGH≥1/2SABCD.SEFGH≥1/2SABCD.
tk
Gọi H′H′ là hình chiếu của H trên BC và G′G′ là hình chiếu của G trên AB.
Ta có: SEFGH=1/2EG.HFSEFGH=1/2EG.HF
Và SABCD=AD.CD;SABCD=AD.CD;
EG≥GG′=AD;EG≥GG′=AD;
HF≥HH′=CD.HF≥HH′=CD.
Do đó: SEFGH≥1/2SABCD.SEFGH≥1/2SABCD.

Xét ΔABD có M,Q lần lượt là trung điểm của AB,AD
=>MQ là đường trung bình
=>MQ//BD và MQ=BD/2
Xét ΔCBDcó
N,P lần lượt là trung điểm của CB,CD
=>NP là đường trung bình
=>NP//BD và NP=BD/2
=>MQ//NP và MQ=NP
Xét ΔBAC có M,N lần lượt là trung điểm của BA,BC
=>MN là đường trung bình
=>MN=AC/2=BD/2=MQ
Xét tứ giác MNPQ có
MQ//NP
MQ=NP
=>MNPQ là hình bình hành
mà MN=MQ
nên MNPQ là hình thoi
a: Xét ΔABD có AE/AB=AH/AD
nên EH//BD và EH=BD/2
Xét ΔCBD có CF/CB=CG/CD
nên FG//BD và FG=BD/2
=>EH//FG và EH=FG
=>EHGF là hình bình hành
Xét ΔBAC cos BE/BA=BF/BC
nên EF//AC và EF=AC/2
=>EF vuông góc với BD
=>EF vuông góc với EH
=>EHGF là hình chữ nhật
b: EH=BD/2=2,5cm
EF=AC/2=4cm
=>\(S_{EFGH}=4\cdot2,5=10\left(cm^2\right)\)