Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\hept{\begin{cases}\\\end{cases}\hept{\begin{cases}\\\\\end{cases}}\orbr{\begin{cases}\\\end{cases}}^{ }^2_{ }}\) | |

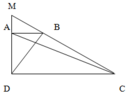
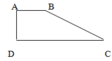
a. S A B C = 1 3 S A D C (Vì cùng chung chiều cao của hình thang ABCD; đáy AB = 1 3 DC)
b. S A B M = S A C M (Vì cùng chung đáy MA, chiều cao AB = 1 3 DC )
c. Theo phần a, ta có: S A B C = S A D C
Mà S A B C D = S A B C + S A D C
Nên S A B C = 1 1 + 3 S A B C D = 1 4 S A B C D
Do đó S A B C D = 64 × 1 4 = 16 ( c m 2 )
Theo phần b, ta có: S A B M = 1 3 S A C M
Mà S A C M = S M A B + S A B C
Nên S M A B = 1 3 - 1 S A B C = 1 2 S A B C
Do đó S M A B = 16 × 1 4 = 8 ( c m 2 )

Xét tam giác ABC và ACD có cùng chiều cao chính là chiều cao hình thang, đáy dc gấp 3 đáy AB => S_ACD gấp 3 lần S_ABC.
Vậy diện tích tam giác ABC là : 16 : (3 + 1) = 4 (cm2)
Xét tam giác MAB và MAC có chung đáy MA mà CD gấp 3 lần AB (vì AB và CD cùng vuông góc với MD) => S_MAB = 1/3 S_MAC => S_MAB = 1/2 S_ABC
Vậy diện tích MAB là : 4 : (3-1) = 2 (cm2)

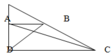
Nối B với D và nối A với C.
Xét 2 tam giác: BAD và CAD. Có:
-Chung đáy AD
-Chiều cao AB = 1 3 CD
=> S.BAD = 1 3 S.CAD
Do đó: S.BAD = 1 4 S.ABCD
S.BAD = 16 : 4 = 4 ( c m 2 )
S.BDC = 16 - 4 = 12 ( c m 2 )
Tam giác BDM và tam giác CDM có chung đáy MD và chiều cao BA = 1 3 CD
Do đó: S.BDM = 1 3 S.CDM
Suy ra S.BDM = 1 2 S.BDC
Mà S.BDC = 12 c m 2 . Nên S.BDM = 12 : 2 = 6 ( c m 2 )
Vì S.MAB = S.BDM - S.BAD . Nên S.MAB = 6 – 4 = 2 ( c m 2 )
Đáp số: S.MAB = 2 ( c m 2 )
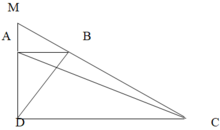
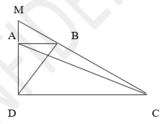

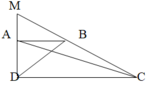

Xét ΔMCD có AB//CD
nên ΔMAB~ΔMDC
=>\(\dfrac{S_{MAB}}{S_{MDC}}=\left(\dfrac{AB}{CD}\right)^2=\dfrac{1}{9}\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot S_{MDC}\)
Ta có: \(S_{MAB}+S_{ABCD}=S_{MDC}\)
=>\(S_{ABCD}=S_{MDC}-\dfrac{1}{9}\cdot S_{MDC}=\dfrac{8}{9}\cdot S_{MDC}\)
=>\(S_{MDC}=64:\dfrac{8}{9}=72\left(cm^2\right)\)
=>\(S_{MAB}=\dfrac{1}{9}\cdot72=8\left(cm^2\right)\)