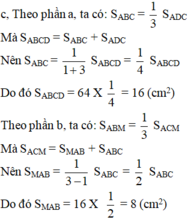Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔNAB vuông tại A và ΔNDC vuông tại D có
\(\widehat{N}\) chung
Do đó: ΔNAB đồng dạng với ΔNDC
=>\(\dfrac{S_{NAB}}{S_{NDC}}=\left(\dfrac{AB}{DC}\right)^2=\dfrac{1}{9}\)
=>\(S_{NAB}=\dfrac{1}{9}\cdot S_{NDC}\)
Ta có: \(S_{NAB}+S_{ABCD}=S_{NDC}\)
=>\(S_{ABCD}=S_{NDC}-\dfrac{1}{9}\cdot S_{NDC}=\dfrac{8}{9}\cdot S_{NDC}\)
=>\(S_{NDC}=S_{ABCD}:\dfrac{8}{9}=64\cdot\dfrac{9}{8}=72\left(cm^2\right)\)
=>\(S_{ANB}=\dfrac{1}{9}\cdot72=8\left(cm^2\right)\)

Xin loi bai nay minh ko ve duoc hinh.Thong cam cho minh nhe !!!
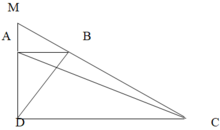
a)S_ABC = 1/3 S_ADC (Đáy AB = 1/3 đáy CD; Chiều cao hạ xuống đáy từ C bằng chiều cao hạ từ A)
b)S_ABM = 1/3 S_CAM (Đáy AM chung; chiều cao hạ từ B bằng 1/3 chiều cao hạ từ B xuống đáy AM)
c)
S_ABC = 1/3 S_ACD (câu trên) => S_ABC = 1/4 S_ABCD = 64 : 4 = 16 cm2
Mà: S_ABM = 1/3 S_ACM (câu trên) => S_ABM = 1/2 S_ABC = 16 : 2 = 8 cm2

Bài giải
a) Do đề bài không cập nhật độ dài của hình thang ABCD nên ta gọi chiều cao là AD ( với AD = BC ), độ dài cạnh DC là 13 ×3=1cm. Vậy, diện tích hình tam giác ABC là :
13 ×AD2 =16 AD( cm2 )
Diện tích hình tam giác ADC là :
\(\frac{1\times AD}{2}=\frac{1}{2}AD\left(cm^2\right)\)
Vì : \(\frac{1}{6}AD< \frac{1}{2}AD\)
nên diện tích hình tam giác ADC lớn hơn diện tích hình tam giác ABC.