Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử hình thang ABCD có đáy nhỏ AB = 15cm, cạnh bên AD = BC = 25cm

Mà ∆ ADH = ∆ BCK (cạnh huyền, cạnh góc vuông)
Suy ra: DH = CK = 12,5 (cm)
Chu vi hình thang ABCD là:
AB + BC + CD + DA = AB + BC + (CK + KH + HD) + DA
= 15 + 25 + (12,5 + 15 + 12,5) + 25 = 105 (cm)
Chu vi hình thang ABCD là:
![]()

gọi hình thang đó là ABCD (AB//CD),AB=15, AD=BC=25
góc DAB=góc ABC=120 độ.
kẻ AH, BK vuông góc với CD (H,K thộc CD)
=>HK=AB=15 (cm)
xét tam giác AHD có: AD=25, góc D=60 độ
=>DH=AD.cos=AD/2=12.5 (cm)
tương tự ta có CK=12.5 (cm)
=>CD=CK+DH+HK=12.5+12.5+15=40 (cm)
=>chu vi ABCD=AB+BC+CD+DA=105 (cm)
gọi hình thang đó là ABCD (AB//CD),AB=15, AD=BC=25
góc DAB=góc ABC=120 độ.
kẻ AH, BK vuông góc với CD (H,K thộc CD)
=>HK=AB=15 (cm)
xét tam giác AHD có: AD=25, góc D=60 độ
=>DH=AD.cos=AD/2=12.5 (cm)
tương tự ta có CK=12.5 (cm)
=>CD=CK+DH+HK=12.5+12.5+15=40 (cm)
=>chu vi ABCD=AB+BC+CD+DA=105 (cm)

gọi hình thang đó là ABCD (AB//CD),AB=15, AD=BC=25
góc DAB=góc ABC=120 độ.
kẻ AH, BK vuông góc với CD (H,K thộc CD)
=>HK=AB=15 (cm)
xét tam giác AHD có: AD=25, góc D=60 độ
=>DH=AD.cos=AD/2=12.5 (cm)
tương tự ta có CK=12.5 (cm)
=>CD=CK+DH+HK=12.5+12.5+15=40 (cm)
=>chu vi ABCD=AB+BC+CD+DA=105 (cm)

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm

\(A=0.5\cdot4\sqrt{3-x}-\sqrt{3-x}-2\sqrt{3}+1=\sqrt{3-x}-2\sqrt{3}+1\) (xác định khi x=<3)
a)thay \(x=2\sqrt{2}\)vào a ra có
\(\sqrt{3-2\sqrt{2}}-2\sqrt{3}+1=\sqrt{\left(\sqrt{2}-1\right)^2}-2\sqrt{3}+1\)
\(=\sqrt{2}-1+2\sqrt{3}+1=\sqrt{2}+2\sqrt{3}\)
Để A=1<=> \(\sqrt{3-x}-2\sqrt{3}+1=1\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}+1-1=0\\ \Leftrightarrow\sqrt{3-x}-2\sqrt{3}=0\\ \Leftrightarrow3-x=12\Leftrightarrow x=-9\)

đề : Cho đoạn thẳng AB cùng điểm C thuộc đoạn thẳng đó (C khác A và B). Về cùng một nửa mặt phẳng bờ AB, kẻ hai tia Ax và By cùng vuông góc với AB. Trên tia Ax lấy điểm M cố định. Kẻ tia Cz vuông góc với tia CM tại C, tia Cz cắt tia By tại K. Vẽ đường tròn tâm O đường kính MC cắt MK tại E

\(T=x^4+y^4+z^4\)
áp dụng bđt bunhia cốp -xki với bộ số \(\left(x^2,y^2,z^2\right);\left(1,1,1\right)\)
\(\left(\left[x^2\right]^2+\left[y^2\right]^2+\left[z^2\right]^2\right)\left(1^2+1^2+1^2\right)\ge\left(x^2+y^2+z^2\right)^2\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(2xy+2yz+2xz\right)^2}{3}\)(bđt tương đương)
\(\left(x^4+y^4+z^4\right)\ge\frac{4}{3}\)
dấu "=" xảy rakhi và chỉ khi
\(\hept{\begin{cases}\frac{x^2}{1}=\frac{y^2}{1}=\frac{z^2}{1}\\x=y=z=1\end{cases}< =>\frac{1^2}{1}=\frac{1^2}{1}=\frac{1^2}{1}}\)(luôn đúng)
vậy dấu "=" có xảy ra
\(< =>MIN:T=\frac{4}{3}\)
sửa dòng 3 dưới lên
\(T\ge\frac{\left(xy+yz+xz\right)^2}{3}=\frac{1}{3}\)
Dấu ''='' xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\)
Vậy GTNN T là 1/3 khi \(x=y=z=\frac{\sqrt{3}}{3}\)
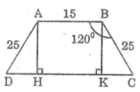



Gọi hình thang đó là ABCD (AB//CD)
AB=15
AD=BC=25 góc
DAB=góc ABC=120 độ.Kẻ AH,BK vuông góc với CD (HK \(\varepsilon\)CD) \(\Rightarrow\)HK=AB=15(cm)
Xét tam giác AHD có:AD=25;Góc D=60 độ \(\Rightarrow\)DH=AD.\(\cos\)=\(\frac{AD}{2}\)=12.5(cm)
Tương tự ta có CK=12.5(cm) \(\Rightarrow CD\)=CK+DH+HK=12.5+12.5+15=40(cm)
\(\Rightarrow\)Chu vi ABCD=AB+BC+CD+DA=105(cm)
105 cm nhé bạn