Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAQP có
A là trung điểm của MQ
B là trung điểm của MP
Do đó: AB là đường trung bình của ΔAQP
Suy ra: AB//QP
Xét hình thang MNPQ có
A là trung điểm của MQ
C là trung điểm của NP
Do đó: AC là đường trung bình của hình thang MNPQ
Suy ra: AC//QP//MN

a: Xét hình thang MNPQ có
A là trung điểm của MQ
B là trung điểm của NP
Do đó: AB là đường trung bình của hình thang MNPQ
Suy ra: AB//MN//PQ
Xét ΔQMN có AI//MN
nên \(\dfrac{AI}{MN}=\dfrac{AQ}{QM}=\dfrac{1}{2}\left(1\right)\)
Xét ΔPMN có KB//MN
nên \(\dfrac{KB}{MN}=\dfrac{1}{2}\left(2\right)\)
Từ (1) và (2) suy ra AI=KB

1: Xét ΔNMP có NA/NM=NB/NP
nên AB//MP và AB=MP/2
Xét ΔQMP có QC/QP=QD/QM
nên DC//MP và DC=MP/2
=>AB//DC và AB=DC
=>ABCD là hình bình hành


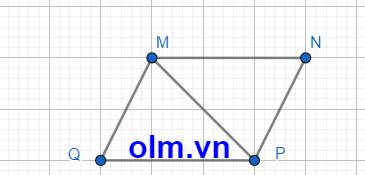
Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
\(\widehat{QPM}\) = \(\widehat{PMN}\) (2 góc so le trong)
\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)
\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)
\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)
b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:
MP chung
MN = PQ
\(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)
⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)
\(\Rightarrow\) MQ = NP (đpcm)
⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\)
Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:
QM // NP (đpcm)