Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi AH là chiều cao của hình thang.
Diện tích hình thang : \(\frac{1}{2}\)AH x ( AB + 2AB ) ( 2AB = CD theo giả thiết)
Diện tích tam giác ABC : \(\frac{1}{2}\)AH x AB
Diện tích tam giác ACD : \(\frac{1}{2}\)AH x 2AB
Ta gọi AM là chiều cao của hình thang.
Ta có:
Diện tích tam giác ABC bằng : (AB * AM):2
Diện tích tam giác ACD bằng: (2 * AB * AM):2
Vậy diện tích tam giác ABC bằng 1/2 diện tích tam giác ACD.
Diện tích tam giác ABC là:
612 : (2+1) * 1=204
Diện tích tam giác ACD là:
612-204=408
Đáp số : 204
408
GHI CHÚ:DẤU * LÀ DẤU NHÂN.
CHÚC BẠN HỌC TỐT NHA!

Lời giải:
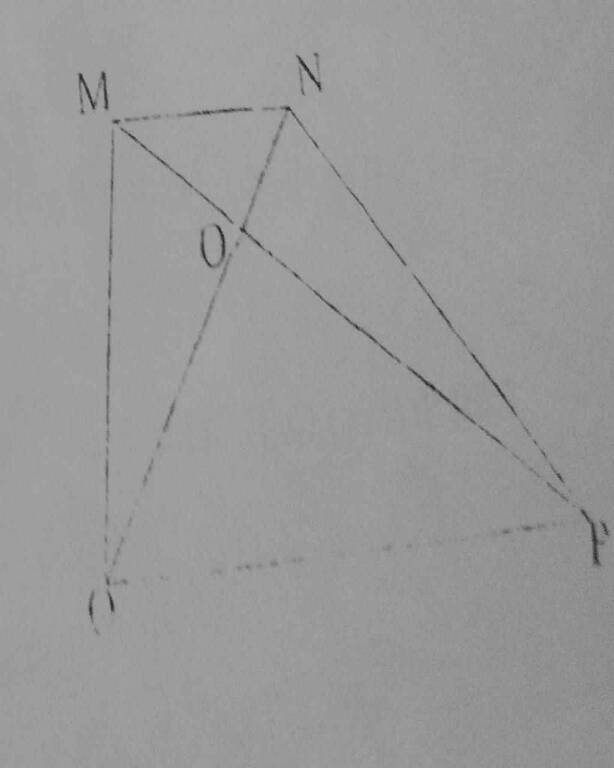
$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)
$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm2)
Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$
\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)
\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)
\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)
Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$
$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$
$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm2)
$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$
$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm2)
Diện tích hình thang:
$15+15+9+25=64$ (cm2)