Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giac ADC và tam giác BDC có :
AC=BD
góc ACD =BDC
Cạnh CD chung

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC

a) Do MN, NP, PQ, QM lần lượt là các đường trung bình các tam giác ABC, ACD, BDC, ABD
=> MN//BC, NP//AD, QP//BC, QM//AD => MNPQ là hình bình hành
b) Do AB//CD => \(\widehat{AMP}=\widehat{CPM}\)
Từ câu trên => \(\widehat{QMP}=\widehat{NPM}\)
Từ 2 điều trên => \(\widehat{AMI}=\widehat{CPN}\)
Mà \(\widehat{MAI}=\widehat{PCN}\)=> T/g AMI đồng dạng t/g CPN
c) Gọi giao AD và BC là E, giao OE và CD là P', giao OE và AB là M'
Ta có AM'/P'C = OM'/OP' = M'B/DP'
AM'/DP' = EM'/ EP' = M'B/P'C
Từ 2 điều trên => DP'/P'C = P'C/DP' => P'D = P'C => P' trùng P mà AM'/M'B = DP/PC = 1
=> M' trùng M ( đây còn là bổ đề hình thang gồm ngược và đảo )
=> M,O,P thẳng hàng (đpcm)

Gọi giao điểm của AC và BD là O
Vì ABCD là hình thang cân nên tam giác AOB cân tại O mà ˆAOB=600⇒AOB^=600⇒ tam giác AOB đều, ta giác COD đều
Mặt khác:
BM là đường cao của tam giác AOB nên BM cũng là trung tuyến ⇒⇒ MA=MO
CN là đường cao của tam giác COD nên cn cũng là trung tuyến⇒ NO=ND
Tam giác AOD có: MA=MO, NO=ND ⇒MN=AD/2
Tam giác BMC vuông tại M có MP là trung tuyến nên \(MP=\frac{BC}{2}=\frac{AD}{2}\)
Tam giác BNC vuông tại N có NP là trung tuyến nên \(NP=\frac{BC}{2}=\frac{AD}{2}\)
Do đó: MN=NP=MP
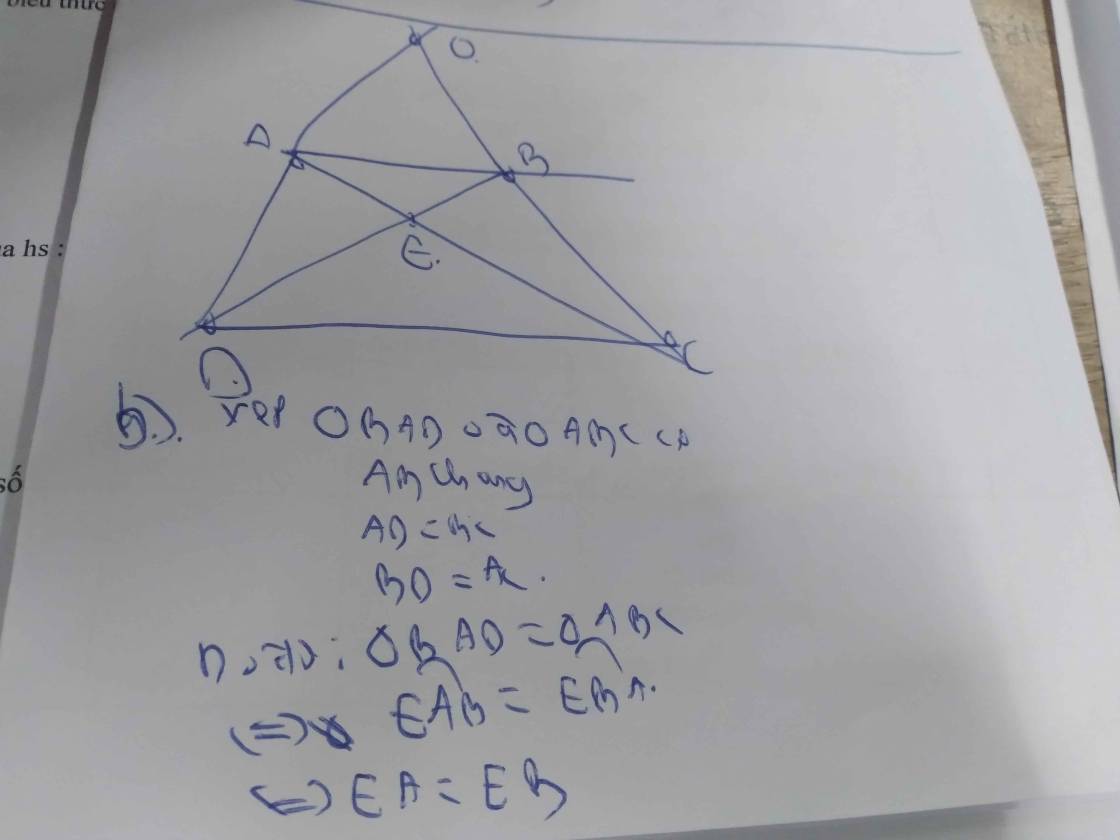

vẽ hình thử đi rồi biết !