Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D H K 2 5
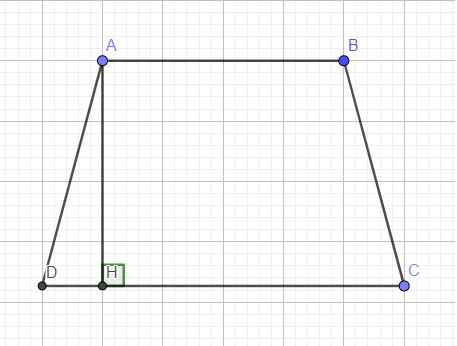
Kẻ AH và BK vuông góc với CD ta có:
AH//BK mà AB//HK nên ABKH là hình bình hành
Ta có góc H = góc K = 90 độ suy ra hình bình hành ABKH là hình chữ nhật
Suy ra HK=AB=2 (cm) nên DH+CK=CD-HK=5-2=3 (cm)
Xét tam giác AHD và tam giác BKC ta có:
góc H = góc K =90 độ
góc D = góc C (ABCD là hình thang cân)
AD=BC (ABCD là hình thang cân)
Do đó tam giác AHD = tam giác BKC ( cạnh huyền - góc nhọn)
Suy ra DH=CK (2 cạnh tương ứng)
Suy ra DK= 3/2=1.5
Ta lại có góc DAH + góc HAB = góc A
nên góc DAH = góc A - góc HAB = 127-90= 37 độ
tan góc DAH = \(\frac{DH}{AH}\) suy ra AH= \(\frac{DH}{\tan DAH}\)
=\(\frac{1,5}{\tan37}\approx2\left(cm\right)\)
SABCD = \(\frac{\left(AB+CD\right)\cdot AH}{2}=\frac{\left(2+5\right)\cdot2}{2}=7\left(cm^2\right)\)

Kẻ đường cao AH ứng với CD
Do ABCD là hình thang cân
\(\Rightarrow DH=\dfrac{CD-AB}{2}=3\left(cm\right)\)
Trong tam giác vuông ADH ta có:
\(tanD=\dfrac{AH}{DH}\Rightarrow AH=DH.tanD=3.tan75^0=6+3\sqrt{3}\left(cm\right)\)
\(S_{ABCD}=\dfrac{1}{2}AH.\left(AB+CD\right)\approx168\left(cm^2\right)\)

A B C D 2cm 60cm H E 6cm F E H
Mik ghi ý th, bạn tự giải chi tiết nha
a)Vẽ BE//AD,BH vuông góc CD.
CM đc ABED là hình bình hành => DE=2,EC=4
Tam giác BEC vuông tại B và có góc C =30 nên BE=EC:2=4:2=2
=>AD=BE=2
b)
Tam giác BEH vuông tại H có EBH=30 =>EH=BE/2=2:2=1
Dùng định lý PTG ta tính đc đường cao rồi tính đc diện tích nha.

Qua điểm C vẽ đường thẳng song song với DB, cắt AB tại E.
=> DCEB là hình bình hành.
Do AC vuông góc với DB nên CE vuông góc với AC.
Hay ▲ACE vuông tại C.
Kẻ CH vuông góc với AB, ta có :
CH2 = AH . EH = 9.9 = 81
=> CH = 9 (cm)
=> SABCD = \(\frac{1}{2}\)CH(AB + CD) = 81 (cm2)