Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ∆ACD và ∆BDC ta có :
DC chung
BC = AD (ABCD là hình thang cân )
ADC = BCD ( ABCD là hình thang cân)
=> ∆ACD = ∆BDC (c.g.c)
=> BDC = ACD (tg ứng)
=> ∆DOC cân tại O
=> OC = OD
Mà AB//DC
ABO = ODC ( so le trong)
BAO = OCN (so le trong)
Mà BDC = ACD (cmt)
=> OAB = ABO
=> ∆AOB cân tại O
=> OA = OB
b) Xét ∆OND và ∆ONC ta có
OC = OD (cmt)
ODC = ONC (cmt)
ON chung
=> ∆OND = ∆ONC (c.g.c)
=> DN = NC(1)
Mà OND + ONC = 180 độ( kề bù)
Mà OND = ONC = 180/2 = 90 độ
=> ON vuông góc với AC(2)
Từ (1) và (2) ta có ∆ cân AOB có trung trực OM đồng thời có trung tuyến OM (3)
Chứng minh tương tự ta có :
∆OMA = ∆OMB
=> AM = MB(4)
=> OMB + OMA = 180 độ(kề bù )
=> OMB = OMA = 180/2 = 90 độ
=> OM vuông góc với AB(5)
Từ (4) và(5) ta có :∆ cân DOC có trung trực ON đồng thời là trung tuyến ON (6)
Từ (3) và (5) => M , O , N thẳng hàng

a: Xét ΔACD và ΔBDC có
AC=BD
AD=BC
CD chung
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
hay \(\widehat{ODC}=\widehat{OCD}\)
Xét ΔOCD có \(\widehat{ODC}=\widehat{OCD}\)
nên ΔOCD cân tại O
Suy ra: OC=OD
Ta có: OC+OA=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB


a) ABCD là hình thang nên AB//CD
CD=2AB ==>AB/CD=1/2
AB//CD, áp dụng định lý Ta-let, ta có
OA/OC=OB/OD=AB/CD=1/2
=>OA/OC=1/2 => OC=2OA
B) Ta có : OA/OC=OB/OD=AB/CD=1/2
==> OD/OB = 2 ==>OD = 2OB
*xét: OC/AC = 2OA/(OA + OC) = 2OA/(OA + 2OA) = 2OA/3OA = 2/3(1);
OD/BD = 2OB/(OD + OB) = 2OB/(2OB + OB) = 2/3(2)
*từ (1),(2) =>OC/AC = OD/BD = 2/3
=>O là trọng tâm tam giác FCD
c)
Vì một đường thẳng song song với AB và CD lần lượt cắt các đoạn thẳng AD, BD,AC và BC tại M, I,K và N nên KN//AB ,IM//AB và IN//AB
MI//AB, áp dụng hệ quả của định lý Ta-let, ta có
MI/AB = DM/AD = DI/IB (1)
IN//AB, áp dụng định lý Ta-let, ta có
CN/BC=DI/IB (2)
Từ (1) và (2), ta có
DM/AD=CN/BC
d)
KN//AB, áp dụng hệ quả của định lý Ta-let, ta có
KN/AB=CN/BC
Ta có :KN/AB=CN/BC và MI/AB=DM/AD
mà DM/AD=CN/BC nên KN/AB=MI/AB => KN=MI

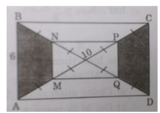
a) Ta có MN và PQ lần lượt là các đường trung bình của các tam giác AOB và COD mà AB // CD và AB = CD nên MN // PQ và MN = PQ
⇒ Tứ giác MNPQ là hình bình hành.
Tương tự NP // BC mà AB ⊥ BC nên MN ⊥ NP. Do đó MNPQ là hình chữ nhật.
Trong ΔABC ta có

Vậy SMNPQ = MN.PQ = 3.4 = 12 (cm2).
b)Dễ thấy ΔAOB = ΔCOD (c.c.c).
Tương tự ΔMON = ΔPOQ
Do đó: SAOB = SCOD và SMON = SPOQ.
⇒ SAOB - SMON = SCOD - SPOQ hay SAMNB = SCPQD.