Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có CD=2AB=2AD=>AB=AD=CD/2=MB=MC.
tứ giác ABCM có AB//MC(vì AB//CD)
AB=MC. do đó: tứ giác ABCD là hình bình hành,=>AM=BC=AD
tam giác ADM có AD=AM=DM nên là tam giác đều
Ta có: Xét tứ giác ABCM có AB//CM (M thuộc DC), AB=CM (=1/2CD)
=> Tứ giác ABCM là hình bình hành => AM=BC
Mà BC=AD (ABCD là hình thang cân) => AM=AD=DM (DM=1/2DC)
Vậy ADM là tam giác đều.

a: Xét tứ giác ABHD có
\(\widehat{BAD}=\widehat{ADH}=\widehat{BHD}=90^0\)
=>ABHD là hình chữ nhật
Hình chữ nhật ABHD có AB=AD
nên ABHD là hình vuông
=>AB=BH=HD=DA
mà \(AB=AD=\dfrac{DC}{2}\)
nên \(BH=DH=\dfrac{DC}{2}\)
DH=DC/2
=>H là trung điểm của DC
Xét ΔDBC có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔDBC cân tại B(2)
Xét ΔBDC có
BH là đường trung tuyến
\(BH=\dfrac{DC}{2}\)
Do đó: ΔBDC vuông tại B(1)
Từ (1) và (2) suy ra ΔBDC vuông cân tại B
b: AB=HD
HD=HC
Do đó: AB=HC
Xét tứ giác ABCH có
AB//CH
AB=CH
Do đó: ABCH là hình bình hành
=>AC cắt BH tại trung điểm của mỗi đường
mà M là trung điểm của BH
nên M là trung điểm của AC
c: \(\widehat{ADI}+\widehat{IAD}=90^0\)(ΔADI vuông tại I)
\(\widehat{ACD}+\widehat{IAD}=90^0\)(ΔADC vuông tại D)
Do đó: \(\widehat{ADI}=\widehat{ACD}\)
mà \(\widehat{ACD}=\widehat{BAC}\)(hai góc so le trong, AB//CD)
nên \(\widehat{BAC}=\widehat{ADI}\)
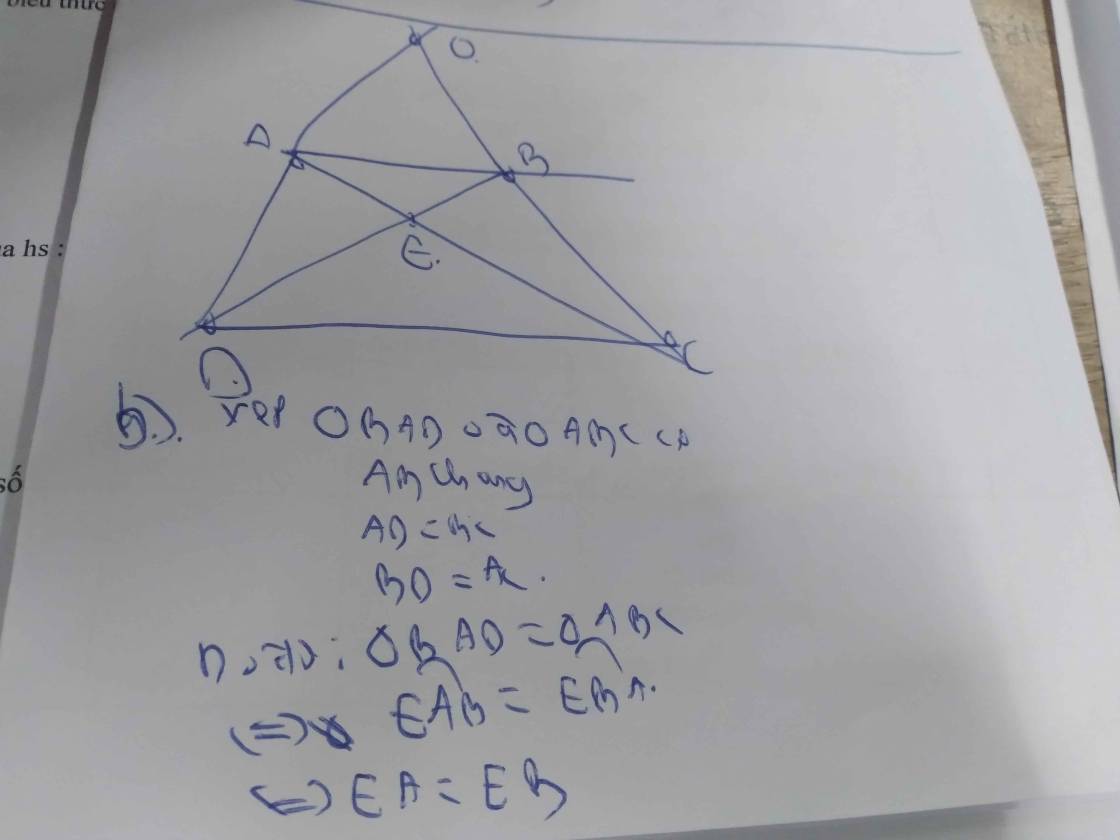

Bn tự vẽ hình nhé =))
Xét hình thang ABCD cân ta có :
\(AB=AD=\frac{1}{2}CD\)
mà DM = DC
=) DM = AD
=) Tam giác ADM cân tại D
minh làm dk n phải đợi lâu lắm