Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B E I C D H
Xét hình thang ABCD có
\(\widehat{C}=\widehat{D}=80^o\) => ABCD là hình thang cân => AD=BC
\(\Rightarrow\widehat{A}=180^o-\widehat{D}=180^o-80^o=100^o\) (Hai góc trong cùng phía)
Tương tự ta cũng có \(\widehat{B}=100^o\)
\(\Rightarrow\widehat{A}=\widehat{B}=100^o\)
Xét tg ABC và tg ABD có
AD=BC (cmt)
\(\widehat{A}=\widehat{B}\) (cmt)
AB chung
=> tg ABD = tg ABC (c.g.c) \(\Rightarrow\widehat{ADB}=\widehat{ACB}\)
Mà \(\widehat{ADB}+\widehat{BDC}=\widehat{ADC}=180^o=\widehat{BCD}=\widehat{ACB}+\widehat{ACD}\)
\(\Rightarrow\widehat{BDC}=\widehat{ACD}=\left(180^o-\widehat{CID}\right):2=60^o\)
=> tg CID là tg đều => CD=CI (1)
Xét tg ABI có
\(\widehat{BAC}=\widehat{ACD}=60^o\) (góc so le trong)
\(\widehat{ABD}=\widehat{BDC}=60^o\) (góc so le trong)
\(\widehat{AIB}=\widehat{CID}=60^o\) (góc đối đỉnh)
=> tg ABI là tg đều
Ta có AE là phân giác \(\widehat{BAI}\) (gt)
=> AE là đường trung trực, đường cao của tg ABI (trong tg đều đường phân giác đồng thời là đường cao, đường trung trực)
Xét tg BIE có
AE đồng thời là đường cao và đường trung trực => tg BIE cân tại E
\(\Rightarrow\widehat{DBC}=\widehat{BIE}\) (góc ở đáy tg cân)
Ta có
\(\widehat{DBC}=\widehat{B}-\widehat{ABD}=100^o-60^o=40^o=\widehat{BIE}\)
=> \(\widehat{BEI}=180^o-\left(\widehat{DBC}+\widehat{BIE}\right)=180^o-\left(40^o+40^o\right)=100^o\)
\(\Rightarrow\widehat{IEC}=180^o-\widehat{BEI}=180^o-100^o=80^o\)
Ta có
\(\widehat{BIC}=180^o-\widehat{CID}=180^o-60^o=120^o\)
\(\Rightarrow\widehat{EIC}=\widehat{BIC}-\widehat{BIE}=120^o-40^o=80^o\)
Xét tg CIE có
\(\widehat{IEC}=\widehat{EIC}=80^o\) => tg CIE cân tại C => CE=CI (2)
Từ (1) và (2) => CE=CD

1/
A B C D H K 1 2,7
Kẻ AH \(\perp\)CD , \(BK\perp CD\)
Xét tam giác vuông AHD và tam giác vuông BKC, có: góc ADH = góc BCK = 600 ; cạnh AH = BK
=> tam giác AHD = tam giác BKC (gcg)
=> DH = KC
Đặt a = DH (a > 0) => AH = \(\sqrt{1-x^2}\)
Có: Sin60 = \(\frac{AH}{AD}\Rightarrow\frac{\sqrt{3}}{2}=\sqrt{1-x^2}\Rightarrow1-x^2=\frac{3}{4}\Rightarrow x^2=\frac{1}{4}\Rightarrow\left[\begin{array}{nghiempt}x=\frac{1}{2}\left(n\right)\\x=-\frac{1}{2}\left(l\right)\end{array}\right.\)
=> x = 1/2 hay DH = KC = 1/2
Mặt khác: HK = CD - (DH + KC) = 2,7 - (1/2 + 1/2) = 1,7 (m)
Tứ giác ABCD là hình chữ nhật (góc AHK = góc BKH = ABK = 900) => AB = HK = 1,7 (m)
Vậy AB = 1,7m
2/
I D C A B 1 2
a/ Cm: tam giác ICD đều:
Trong tam giác ICD : DB vừa là đường phân giác , vừa là đường cao => tam giác ICD là tam giác cân tại D
=> ID = DC (1)
=> DB vừa là đường trung tuyến => BI = BC = 4cm => IC = 4 + 4 = 8cm (2)
Có: góc IAB = IDC (đồng vị) , góc IBA = góc ICD (đồng vị)
mà góc IDC = góc ICD
=> góc IAB = góc IBA => tam giác IAB cân tại I => IA = IB = 4cm
=> ID = IA + AD = 4 + 4 = 8cm (3)
Từ (1), (2), (3) => ID = DC = IC = 8cm hay tam giác IDC đều
b/ Tính chu vi hình thang ABCD:
Vì tam giác ICD đều => tam giác IAB đều => IA = AB = 4cm
ID = DC = 8cm
Vậy chu vi hình thang ABCD : AB + AD + BC + CD = 4 + 4 + 4 + 8 = 20(cm)

em tự vẽ hình
câu 1 em tự chứng minh nhé
câu 2,
ta có IE//BC\(\Rightarrow\widehat{EIC}=\widehat{ICB}\) (so le trong)
mà \(\widehat{ECI}=\widehat{ICB}\) (phân giác )
=> \(\widehat{EIC}=\widehat{ECI}\)
=> tam giác IEC cân tại E
chứng minh tương tự cvới tam giác kia nhé
c)
ta có tam giác IEC cân tại E=> IE=EC
vơi tam giác kia cân thì ta có IF=FB
=> IE+IF=BF+CE
=> EF=BF+IC

A B D C 60*
Xét\(\Delta BCD\)
\(CBD=180-^{BCD}-^{BCD}=180-60-30=90\Rightarrow\Delta BCD\)VUÔNG TẠI A
\(\Rightarrow BC=\frac{CD}{2}\)TAM GIÁC VUÔNG ĐỐI DIỆN GÓC 30Đ=\(\frac{1}{2}\)CẠNH HUYỀN\(\Rightarrow CD=2.BC\left(1\right)\)
+AB//CD\(\Rightarrow\)\(^{ABC}+^{BCD}=^{ABC}+60=180\)
\(\Rightarrow^{ABC}=180-60=120\Rightarrow^{ABD}=^{ABC}-^{CBD}=120-90=30\)
+XÉT \(\Delta ABD\)CÓ\(^{ADB}=^{ABD}=30\Rightarrow\frac{T}{G}ABD\)CÂN TẠI A\(\Rightarrow AD=AB\left(2\right)\)
+DO HÌNH THANG ABCD CÂN \(\Rightarrow\)AD=BC\(\left(3\right)\)
+CHU VI HÌNH THANG \(=AB+BC+CD+AD\left(4\right)\)
TỪ \(\left(1\right)\left(2\right)\left(3\right)\left(4\right)\)=CHU VI HÌNH THANG ABCD =5.BC=20CM
\(\Rightarrow BC=20:5=4CM\)
\(\Rightarrow AB=BC=AD=4CM\)
\(CD=2.BC=2.4=8CM\)

Em tham khảo câu 1 tại link dưới:
Câu hỏi của Thư Anh Nguyễn - Toán lớp 8 - Học toán với OnlineMath

Đáp án cần chọn là: C
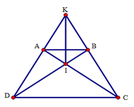
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra A C D ^ = B D C ^ (hai góc tương ứng), suy ra tam giác ICD cân tại I.
Nên C sai vì ta chưa đủ điều kiện để IC = CD
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.
Xét tam giác KDI và tam giác KCI có:
+ KD = KC (do ΔKCD cân tại K))
+ KI là cạnh chung
+ IC = ID
Suy ra ΔKDI = ΔKCI (c.c.c)
Suy ra K D I ^ = C K I ^ , do đó KI là phân giác A K B ^ nên D đúng.
Ta có AB // CD (do ABCD là hình thang) nên K A B ^ = K C D ^ ; K B A ^ = K C D ^ (các cặp góc đồng vị bằng nhau)
Mà K D C ^ = K C D ^ (tính chất hình thang cân) nên K A B ^ = K C D ^ (tính chất hình thang cân) nên hay ΔKAB cân tại K. Do đó A đúng