Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

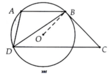
Chứng minh được: ∆DBC:∆BAD => D B C ^ = B A D ^
=> s đ D B C ⏜ = 1 2 s đ B m D ⏜
=> BC là tiếp tuyến của (O)

A B D C M P Q I K R E F
a) Gọi I, K lần lượt là trung điểm của AP và DP. Ta có :
IK song song và bằng 1/2 AD hay bằng 1/2 BC.
KM = DM - DK = DC/2 - DP / 2 = PC/2
Mà \(\widehat{IKM}=\widehat{ADC}=\widehat{BCP}\)
\(\Rightarrow\Delta IKM\sim\Delta BCP\left(c-g-c\right)\Rightarrow\widehat{BPC}=\widehat{IMP}\)
Mà \(\widehat{BPC}=\widehat{ABP}\) (AB // PC) ; \(\widehat{ABP}=\widehat{AQR}\) (Hai góc nội tiếp cùng chắn cung AR)
Do đó \(\widehat{IME}=\widehat{IQE}\Rightarrow\) Tứ giác IMQE nội tiếp.
\(\Rightarrow\widehat{EIQ}=\widehat{EMQ}\)
Mà IE // AF (Đường trung bình) nên \(\widehat{IEQ}=\widehat{FAQ}\) (Đồng vị)
\(\Rightarrow\widehat{FAQ}=\widehat{FMQ}\) hay tứ giác AMQF nội tiếp.
Do đó đường tròn ngoại tiếp tam giác AQF đi qua A, M cố định.
Vậy tâm đường tròn thuộc đường trung trực của AM.
b) Ta có \(\widehat{EPR}=\widehat{BPC}=\widehat{ABP}=\widehat{AQE}\) nên \(\Delta EPR\sim\Delta EQP\left(g-g\right)\Rightarrow\frac{EP}{EQ}=\frac{ER}{EP}\Rightarrow EP^2=ER.EQ\)
Vì AE là tiếp tuyến nên \(\widehat{EAR}=\widehat{AQE}\Rightarrow\Delta EAR\sim\Delta EQA\left(g-g\right)\Rightarrow\frac{EA}{EQ}=\frac{ER}{EA}\Rightarrow EA^2=EQ.ER\)
\(\Rightarrow EP^2=EA^2\Rightarrow EP=EA=EF\)
\(\Rightarrow\widehat{FAP}=90^o\Rightarrow\widehat{FMQ}=90^o\) (Hai góc nội tiếp cùng chắn cung FQ)
\(\Rightarrow MQ\perp CD\)

Ta có : \(\widehat{ACB}=\widehat{CAQ}+\widehat{CQA}\Rightarrow\widehat{CQA}=\widehat{ACB}-\widehat{CAQ}\)
Mà \(\widehat{ACB}=\frac{1}{2}sđ\widebat{AB}\); \(\widehat{CAQ}=\frac{1}{2}sđ\widebat{AC}\)( do AQ là tiêp tuyến của ( O ) )
BD = AB \(\Rightarrow sđ\widebat{AB}=sđ\widebat{BD}\)
Ta có : \(\widehat{ACB}-\widehat{CAQ}=\frac{1}{2}sđ\widebat{AB}-\frac{1}{2}sđ\widebat{AC}=\frac{1}{2}sđ\widebat{BD}-\frac{1}{2}sđ\widebat{AC}=\widehat{CRA}\)
Suy ra : \(\widehat{CRA}=\widehat{AQC}\) \(\Rightarrow\)tứ giác ARQC nội tiếp
\(\Rightarrow\widehat{QRC}=\widehat{QAC}\)
Mà \(_{\widehat{QAC}=\widehat{ADC}}\)\(\Rightarrow\widehat{QRC}=\widehat{ADC}\)
\(\Rightarrow QR//AD\)