Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ai trả lời đc tui cho 1 acc liên quân cấp 30 có 16 tướng và 6 trang phục
tự vẽ hình , k ib mk vẽ hình cho
a)
xét tam giác AHD vuông và tam giác vuông BKC có AD=BC( hình thang cân )
góc D= góc C ( hình thang cân )
=> tam giác AHD = tam giác BKC ( trường ohjwp cạnh huyền canh góc vuông )
=> DH=CK
b)
có AB//HK ; AH//BK (cùng vuông góc DC=>//) và AHK= 90 độ => ABKH là hcn => AB=HK=10cm và ABKH là hcn => AH=BK
có DH+CK+HK=DC
=> mà DH=Ck => 2CK+HK=CD => 2CK+10=26=> 2CK=16=>CK=8
có tam giác BKC vuông tại K => \(BK^2+KC^2=BC^2\)
=> \(BK^2=BC^2-KC^2\)
\(\Rightarrow BK^2=17^2-8^2\)
\(\Rightarrow BK^2=225\Rightarrow BK=15\)
mà BK=AH ( mình chứng minh ở trên r đó b lướt lên là thấy )
=> AH=15
add acc lq nha , k cần ,add đưa nik lq , >.< <3


\(a,\widehat{D}=\widehat{C}=70^0\left(t/c.hthang.cân\right)\\ AB//CD\Rightarrow\widehat{A}+\widehat{D}=180^0\left(2.góc.trong.cùng.phía\right)\Rightarrow\widehat{A}=110^0\\ \widehat{A}=\widehat{B}=110^0\left(t/c.hthang.cân\right)\\ b,\left\{{}\begin{matrix}AD=BC\left(t/c.hthang.cân\right)\\\widehat{AHD}=\widehat{BKC}\left(=90^0\right)\\\widehat{D}=\widehat{C}\left(cm.trên\right)\end{matrix}\right.\Rightarrow\Delta AHD=\Delta BKC\left(ch-gn\right)\Rightarrow DH=CK\)


Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
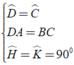
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)

Bài 8:
a: Xét ΔDBC có
E là trung điểm của BD
M là trung điểm của BC
Do đó: EM là đường trung bình của ΔDBC
Suy ra: EM//DC
b: Xét ΔAEM có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
Bài 5:
Xét ΔABC có
\(\dfrac{AE}{EB}=\dfrac{AD}{DC}\left(=1\right)\)
Do đó: DE//BC
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
A B D C H K
a/
Xét tg vuông ADH và tg vuông BCK
Do ABCD là hình thang cân
=> AD=BC; \(\widehat{ADC}=\widehat{BCD}\) => tg ADH = tg BCK (Hai Tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
=> DH = CK
b/
\(AH\perp CD;BK\perp CD\) => AH//BK
Mà AH = BK (đường cao của hình thang)
=> ABKH là hình bình hành
=> AB = HK = 6 cm (cạnh đối hbh)
=> DH+CK=CD-HK=10-6=4 cm
Mà DH = CK => DH=CK=2cm
Xét tg vuông ADH
\(AD=\sqrt{DH^2+AH^2}\)
Bài toán thiếu dữ kiện không tính được AH
ABCD là tg cân