Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ ta có E là trung điểm của AB => EF là đường trung bình trong tam giác ABC
F là trung điểm của AC
=> EF // BC (1)
+H là trung điểm của BD => HG là đường trung bình trong tam giác BDC
G là trung điểm CD
=> HG//BC(2)
từ (1) và (2) => EF//HG(*)
+ E là trung điểm AB; H là trung điểm BD=> EH là đường trung bình trong tam giác BAD=>EH//AD(3)
+ F là trung điểm của AC; G là trung điểm của CD=> FG là đường trung bình trong tam giác CAD=>FG//AD(4)
từ (3) và (4) => EH//FG(**)
từ (*) và (**) => tứ giác EFGH là hình bình hành ( LÀ HÌNH THOI CƠ BN NHƯNG MK ĐANG BẬN NÊN BN CỐ GẮNG CM TIẾP NHÉ!!!)

a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔBCD có
F là tđiểm của BC
G là tđiểm của CD
Do đó: FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Xét ΔADC có
H là tđiểm của AD
G là tđiểm của CD
Do đó: GH là đường trung bình
=>GH⊥EH(3)
Từ (1), (2) và (3) suy ra EFGH là hình chữ nhật

đó là hình bình hành đó bạn ơi.
- Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1)
- Nối AC thì sẽ có HG và EF là đường tb của tam giác DCA và BAC => EF//HG vì cùng //AC và bằng 1/2 AC (2)
Từ (1) và (2) => tứ giác HEFG là HBH (có các cặp cạnh // và bằng nhau từng đôi một)
Chúc bạn thành công...
tk nha bạn
thank you bạn
a, Ta noi AC lai voi nhau .
Xet tam giac ABD co :
AH=HD a AE=EB
=> HE la dtb => HE=1/2BD va HE//DB (1)
Xet tam giac BDC co :
DG=GC va BF=FC
=> GF la dtb => GF=1/2BD va GF//BD (2)
Tu (1) va (2) suy ra : HE//GF va HE=GF
Hay tứ giác EFGH la HBH
b, Nếu AC vuông góc với BD thì tứ giác EFGH là hình HCN vì :
Ta có : AC//EF va BD//HE
=> E=90
Hay hình bình hành EFGH là hình chữ nhật ( hình bình hành có 1 góc vuông là hình chữ nhật)
c, Áp dụng định lý pi-ta-go là :
AO2+OB2=AB2
x2+82=102
x2=102-82
x2=36
=>x=6
Dien h tam giac AOB la :
\(\frac{1}{2}.6.8=24cm^2\)
Vay dien h tam giac AOB la 24cm2
Câu a bạn có thể kham khảo bài của bạn le anh tu (co 2 cach)
nho k nha

a: Xét ΔABC có
E là trung điểm của AB
H là trung điểm của AC
Do đó: EH là đường trung bình của ΔABC
Suy ra: EH//BC và EH=BC/2(1)
Xét ΔBDC có
F là trung điểm của BD
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔBDC
Suy ra: FG//BC và FG=BC/2(2)
Xét ΔABD có
E là trung điểm của AB
F là trung điểm của BD
Do đó: EF là đường trung bình của ΔABD
Suy ra: EF//AD và EF=AD/2
hay EF=BC/2(3)
Từ (1) và (2) suy ra EH//FG và EH=FG
Từ (2) và (3) suy ra EF=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
mà EF=FG
nên EHGF là hình thoi

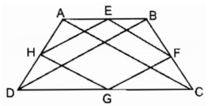
Trong ∆ ABD ta có:
E là trung điểm của AB (gt)
H là trung điểm của AD (gt)
nên EH là đường trung bình của ∆ ABD
⇒ EH // BD và EH = 1/2 BD (tính chất đường trung bình của tam giác) (1)
- Trong ∆ CBD ta có:
F là trung điểm của BC (gt)
G là trung điểm của CD (gt)
nên FG là đường trung bình của ∆ CBD
⇒ FG // BD và FG = 1/2 BD (tính chất đường trung bình của tam giác) (2)
Từ (1) và (2) suy ra: EH // FG và EH = FG
Suy ra: Tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Trong ∆ ABC ta có:
EF là đường trung bình
⇒ EF = 1/2 AC (tính chất đường trung bình của tam giác) (3)
AC = BD (tính chất hình thang cân) (4)
Từ (1), (3) và (4) suy ra: EH = EF
Vậy : Tứ giác EFGH là hình thoi.

ΔDFG= ΔCHG(GD=GC;DF=CH;góc FDG=gócHCG)
=>GF=GH(1)
ΔEFB= ΔEHA(FB=HA;EB=EA;gócEAH=gócABF)
=>EF=EH(2)
TỪ 1 và 2=> tứ giác EFGH là hình thoi