Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong hình thang cân ABCD (AB//CD) đặt m là sđ góc D (m<180 độ ) thì:D=C=m và A=B=180 độ-m
Tam giác ABD cân tại A =>^ABD=^ADB
AB//CD tạo với cát tuyến BD 2 góc so le trong ^ABD=^CDB
Suy ra ^ADB=^CDB,lại có tia DB nằm giữa 2 tia DA và DC nên tia DB là tia phân giác ^ADC=m độ
Vậy ^ABD= (1/2).m
Tam giác BCD cân tại D =>^DBC=^DCB=m độ
Tia BD nằm giữa 2 tia BA,BC nên ^ABC=^ABD+^DBC=(1/2).m+m (độ)
=(3/2).m (độ)
Mà ^ABC=180-m (độ),nên (3/2).m(độ)=180-m(độ)
hay 5/2.m=180 độ => m=360độ:5=72 độ
và 180 độ-m=108 độ
Trả lời : Trong hình thang cân ABCD kể trên,sđ 2 góc nhọn C và D là 72 độ,sđ 2 góc còn lại là 108 độ

a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
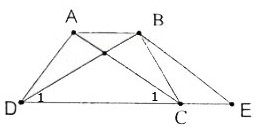
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 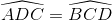
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:

AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 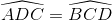
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

Trong hình thang cân ABCD (AB//CD) đặt m là sđ góc D (m<180 độ ) thì:D=C=m và A=B=180 độ-m
Tam giác ABD cân tại A =>^ABD=^ADB
AB//CD tạo với cát tuyến BD 2 góc so le trong ^ABD=^CDB
Suy ra ^ADB=^CDB,lại có tia DB nằm giữa 2 tia DA và DC nên tia DB là tia phân giác ^ADC=m độ
Vậy ^ABD= (1/2).m
Tam giác BCD cân tại D =>^DBC=^DCB=m độ
Tia BD nằm giữa 2 tia BA,BC nên ^ABC=^ABD+^DBC=(1/2).m+m (độ)
=(3/2).m (độ)
Mà ^ABC=180-m (độ),nên (3/2).m(độ)=180-m(độ)
hay 5/2.m=180 độ => m=360độ:5=72 độ
và 180 độ-m=108 độ
Trả lời : Trong hình thang cân ABCD kể trên,sđ 2 góc nhọn C và D là 72 độ,sđ 2 góc còn lại là 108 độ

Đặt
Có: (do tgiác BCD cân
(do tgiác ABD cân)
mà
=> x =
=> 2x =
=> 5x = => x =
Vậy:

Vì ABCD là hình thang cân
=> AD = BD (1)
Vì tam giác ABD là tam giác cân tại A
=> AB = AD (2)
Vì tam giác BCD là tam giác cân
=> BC = AC(3)
Từ (1)(2)(3) ta có
=> AB = BC = CD = AD
=> ABCD là hình vuông
=> A = B = C = D = 90 độ
Vì tam giác ADB cân tại A có ABD = ADB
=> DAB + ADB + ABD = 180 độ
=> ADB + ABD = 180 - DAB
=> ADB + ABD = 90 độ
=> ADB = ABD = 45 độ
Tính tương tự ta có DBC = BDC = 45 độ
vì tam giác DBC cân tại D nên BD = BC .
Vì hình thang ABCD cân nên BC = AD vậy AD = BD mà tam giác ABD là tam giác cân tại dẫn đến ABD là tam giác đều
góc DAB = 60 = goc ABD = goc ADB
vì đây là hình thang nên góc ABD = BDC = 60
vậy góc ADC = 60 + 60 = 120
vì tam giác BDC cân tại D nên góc BDC = BCD = 60
vậy góc ABC bạn tự tính nốt.
bạn vào câu tương tự và tìm câu hỏi của bạn NGUYỄN TẤT ANH QUÂN nha
có câu lời giải đầy đủ!!Vào câu tương tự của bạn Nguyễn Tất Anh Quân
có lời giải liền