Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ lấy hình nha
gọi AC và EF cắt nhau tại I
Ta có : EO // DC ( Vì EF // DC )
Theo định lý Ta let:
\(\frac{ED}{AD}=\frac{OC}{AC}\)
\(\frac{BF}{BC}=\frac{AO}{AC}\)
\(\Rightarrow\)\(\frac{ED}{AD}+\frac{BF}{BC}=\frac{OC}{AC}+\frac{AO}{AC}=1\)
Vậy \(\frac{ED}{AD}=\frac{BF}{AC}=1\left(ĐPCM\right)\)

Gọi O là giao điểm của AC và EF
Xét tam giác ADC có EO //DC
=>AE/AD=AO/AC. (1)
Xét tg ABC có OF//DC
=>CF/CB=CO/CA. (2)
Từ 1 và 2=>AE/AD+CF/CB=AO/AC+CO/CA=AO+CO/AC=AC/AC=1(đpcm)

Xét hình thang ABCD có EF//AB//CD
nên \(\dfrac{AE}{ED}=\dfrac{BF}{FC}\)
=>\(\dfrac{ED}{AE}=\dfrac{CF}{FB}\)
=>\(\dfrac{ED+EA}{AE}=\dfrac{CF+FB}{FB}\)
=>\(\dfrac{AD}{AE}=\dfrac{BC}{FB}\)
=>\(\dfrac{AE}{AD}=\dfrac{BF}{BC}\)
=>\(\dfrac{BF}{BC}=1-\dfrac{ED}{AD}\)
=>\(\dfrac{BF}{BC}+\dfrac{ED}{AD}=1\)

Xét hình thang ABCD có EF//AB//CD
nên AE/ED=BF/FC
=>6/FC=2
hay FC=3(cm)

Bạn tham khảo ở link này nha
https://hoc24.vn/cau-hoi/cho-hinh-thang-abcd-ab-cd-mot-duong-thang-song-song-voi-2-day-cat-canh-ben-ad-bc-theo-thu-tu-o-e-f-tinh-fc-biet-ae-4cm-ed-2cm-bf-6cm.252472345103
https://hoc24.vn/cau-hoi/cho-hinh-thang-abcd-ab-cd-mot-duong-thang-song-song-voi-2-day-cat-canh-ben-ad-bc-theo-thu-tu-o-e-f-tinh-fc-biet-ae-4cm-ed-2cm-bf-6cm.252472345103

Bạn tự vẽ hình nhé
Gọi O là giao điểm của AC và EF
Ta có AE/AD = AO/AC (tam giác ADC có EO//DC)
CF/CB = CO/CA (tam giác ABC có OF//DC)
=> AE/AD + CF/CB = AO/AC + CO/AC = (AO + CO)/AC = AC/AC = 1

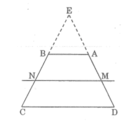
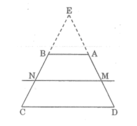
Gọi E la giao điểm của AD va BC
Trong tam giác EMN, ta có: AB // MN (gt)
Suy ra: 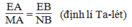
Hay 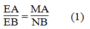
Trong tam giác EDC, ta có: AB // CD (gt)
Suy ra: 
Hay 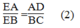
Từ (1) và (2) suy ra : 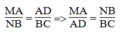
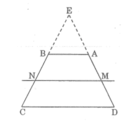
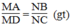

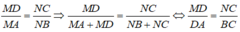
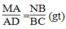
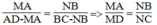
hình tự vẽ ạ
kẻ đường chéo \(AC\), cắt \(EF\) tại H
\(\Rightarrow EH\) // \(DC\) ; \(FH\) // \(AB\)
\(\Delta ADC\) CÓ EH//DC NÊN THEO ĐỊNH LÝ TALET,TA CÓ
\(\frac{AE}{AD}=\frac{AH}{HC}\) \(\left(1\right)\)
\(\Delta ABC\) CÓ HF // AB NÊN THEO ĐỊNH LÝ TALET,TA CÓ:
\(\frac{BF}{FC}=\frac{AH}{HC}\) \(\left(2\right)\)
TỪ \(\left(1\right)\)VÀ \(\left(2\right)\) \(\Rightarrow\frac{AE}{AD}=\frac{BF}{FC}\left(=\frac{AH}{HC}\right)\)(đpcm)