Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Tính các tỉ số AI/DK và BI/DK theo a và b: Từ hình vẽ, ta có thể thấy rằng: ΔAOE ~ ΔCOD (cùng góc AOE và góc COD) ΔBOE ~ ΔAOE (cùng góc BOE và góc AOE) Từ đó, ta có thể suy ra các tỉ số sau: AI/DK = AO/CO = b/a BI/DK = BO/AO = a/b b) Chứng minh AI = BI, CK = DK: Từ các tỉ số trên, ta có thể thấy rằng: AI/DK = b/a BI/DK = a/b Từ đó, ta có thể suy ra rằng: AI = BI (vì AI/DK = BI/DK) CK = DK (vì CK/DK = DK/CK) Vậy, ta đã chứng minh được các điểm cần chứng minh.

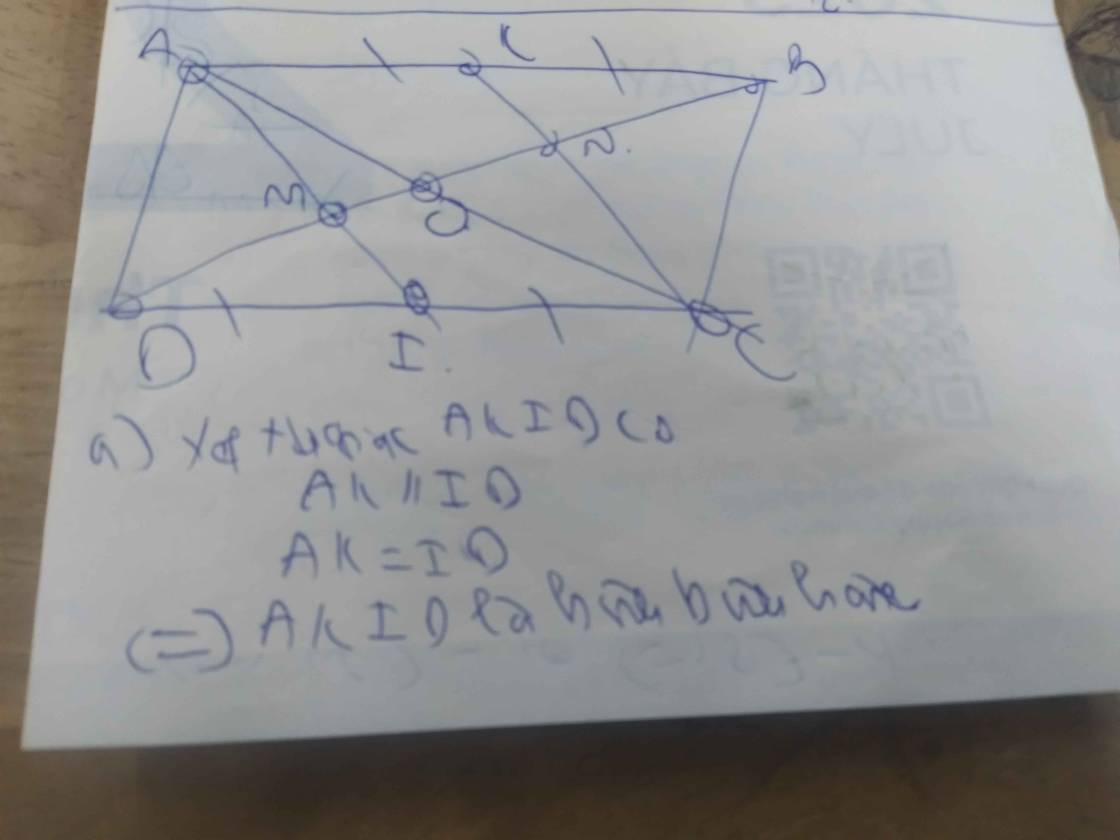
a) Ta có : AB=CD (T/c HBH) mà K là TĐ của AB (gt) và I là TĐ của DC (gt)
Suy ra AK=KB=IC=ID (1) mà K thuộc AB, I thuộc DC nên AK// IC(2)
từ (1) (2) suy ra AKIC là HBH (dhnb) suy ra AI//KC(t/c)(đpcm) mà M thuộc AI, N thuộc KC suy ra AM//KN và MI//NC
b) xét tam giác DNC có: I là TĐ của DC và MI//NC(cmt) suy ra M là TĐ của DN(3)
CMTT suy ra N là TĐ của MB(4)
TỪ (3)(4) suy ra DM=MN=NB(ddpcm)

a: Xét ΔODK có AH//DK
nên AH/DK=OH/OK
Xét ΔOKC có HB//KC
nên HB/KC=OH/OK
=>AH/DK=HB/KC
mà AH=HB
nên DK=KC
=>K là trung điểm của CD
b: Xét ΔMAB và ΔMKD có
góc MAB=góc MKD
góc AMB=góc KMD
Do đo: ΔMAB đồng dạng với ΔMKD
=>MA/MK=AB/DK
=>MK/MA=DK/AB
Xét ΔNKC và ΔNBA có
góc NKC=góc NBA
góc KNC=góc BNA
Do đó: ΔNKC đồng dạng với ΔNBA
=>NK/NB=KC/BA=KD/AB=MK/MA
=>MN//AB

Kẻ đường chéo AC
có E,F,G,H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA
suy ra EF là đường trung bình của tam giác ABC nên EF//=1/2AC (1)
GH là đường trung bình của tam giác ADC nên GH//=1/2AC (2)
Từ (1) và (2) suy ra EF//=GH nên EFGH là hình bình hành
Vì có hai cạnh đối song song và bằng nhau
GOOD LUCK

#) Tự vẽ hình
a) \(\Delta AID=\Delta BKC\left(ch-gn\right)\)
\(\Rightarrow AI=CK\)(2 cạnh tương ứng)
\(\Delta AKB=\Delta CKD\left(ch-gn\right)\)
\(\Rightarrow AI=CK\)(2 cạnh tương ứng)
\(\Rightarrow\)Tứ giác AICK là hình bình hành
a )
Tam giác AID = Tam giác BKC ( cạnh huyền - góc nhọn )
=> AI = CK ( 2 cạnh t.ứ )
Tam giác AKB = Tam giác CKD ( cạnh huyền - góc nhọn )
=> AI = CK ( 2 cạnh tương ứng )
=> Tứ giác AICK là hình bình hành
~ Hok tốt ~
#Deku