Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp
Sử dụng các công thức tính thể tích sau:
+) Thể tích khối nón bán kính đáy r, đường cao h là

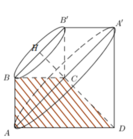
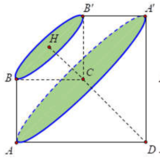
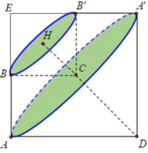
Gọi A’, B’ lần lượt các điểm đối xứng A, B qua CD. H là trung điểm của BB’, ta dễ dàng chứng minh được C là trung điểm của AA’.
Gọi V1 là thể tích khối nón có chiều cao CD, bán kính đáy AC.
V2 là thể tích khối nón cụt có chiều cao CH, bán kính đáy nhỏ BH, bán kính đáy lớn AC.
V3 là thể tích khối nón có chiều cao CH, bán kính đáy BH.

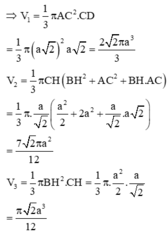


Chọn đáp án A
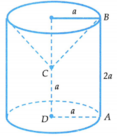
Gọi (T) là khối trụ có đường cao là 2a, bán kính đường tròn đáy là a và (N) là khối nón có đường cao là a, bán kính đường tròn đáy là a
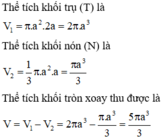

Đáp án A
Ta có thể tích khối tròn xoay tạo thành bằng hiệu thể tích hình trụ bán kính đáy AD, chiều cao CD trừ cho thể tích nón đỉnh B, bán kính đáy BM chiều cao CM.
Ta có
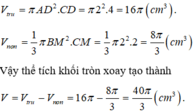
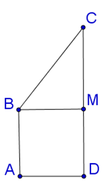

Chọn đáp án A.
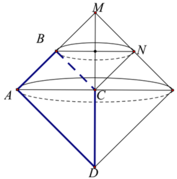
Gọi M là giao điểm của AB và CD. Từ B kẻ đường thẳng song song với AC, cắt CM tại N.
Khi quay ABCD quanh trục CD ta được hai phần:
+ Tam giác ACD sinh ra khối nón với bán kính đáy
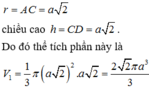


Đáp án A
Gọi V là thể tích của khối tròn xoay cần tính, khi đó V = V 1 − V 2 với
V1 là thể tích khối trụ có chiều cao h 1 = A B , bán kính R = A D → V 1 = π R 2 h 1 = 2 π a 3
V 2 là thể tích khối trụ có chiều cao h 1 = A B − C D , bán kính R = A D → V 2 = 1 3 π r 2 h 2 = π a 3 3
Vậy thể tích cần tính là V = V 1 − V 2 = 2 π a 3 − π a 3 3 = 5 π a 3 3

Đáp án A
Khi quay hình thang ABCD quanh cạnh AB ta được khối nón cụt có
Bán kính hai đáy lần lượt là r = A D = a R = B C = 2 a .
Chiều cao h = A B = a . ⇒ V = π h 3 R 2 + r 2 + R . r = 7 π a 3 3 .




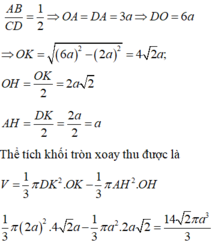
Chọn B