Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có EA = EB; FB = FC
=> EF là đtr/bình của h.thang ABCD
=> EF // AB
Ta có FB = FC; FK // AB
=> FK là đ.tr.bình của t.giác ABC
=> AK = KC
C.minh tương tự ta có BI = ID
b) Ta có KF = AB/2 = 6/2 = 3 cm ( KF là đ.tr.bình của t.giác ABC )
C.minh tương tự ta có EI = 3cm
Ta có EF là đ.tr.bình của h.thang ABCD
=> EF = ( AB + CD )/2 = ( 6 + 10 )/2 = 16/2 = 8 cm
Ta có EF = EI + IK + KF
=> IK = EF - ( EI + KF )
=> IK = 8 - ( 3 + 3 )
=> IK = 2 cm

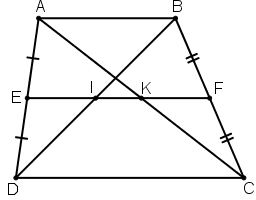
a) Vì EA = ED, FB = FC (gt)
Nên EF là đường trung bình của hình thang ABCD.
Do đó: EF // AB // CD
∆ABC có BF = FC và FK // AB
nên: AK = KC
∆ABD có AE = ED và EI // AB
nên: BI = ID
b) Vi EF là đường trung bình của hình thang ABCD.
nên EF = \(\dfrac{AB+CD}{2}\) = \(\dfrac{6+10}{2}=8\)
EI là đường trung bình của ∆ABD nên \(EI=\dfrac{1}{2}AB=\dfrac{1}{2}.6=3\left(cm\right)\)
KF là đường trung bình của ∆ABC nên \(KF=\dfrac{1}{2}AB=\dfrac{1}{2}.6=3\left(cm\right)\)
Lại có EF = EI + IK + KF
nên IK = EF - (EI + KF) = 8 - (3 + 3) = 2 (cm)
a) + Hình thang ABCD có EA = ED, FB = FC (gt)
⇒ EF là đường trung bình của hình thang ABCD.
⇒ EF // AB // CD
+ ΔABC có BF = FC (gt) và FK // AB (cmt)
⇒ AK = KC
+ ΔABD có: AE = ED (gt) và EI // AB (cmt)
⇒ BI = ID
b) + Vì EF là đường trung bình của hình thang ABCD.
⇒ EF = (AB + CD)/2 = (6 + 10)/2 = 8cm.
+ ΔABD có AE = ED, DI = IB
⇒ EI là đường trung bình của ΔABD
⇒ EI = AB/2 = 6/2 = 3(cm)
+ ΔABC có CF = BF, CK = AK
⇒ KF là đường trung bình của ΔABC
⇒ KF = AB /2 = 6/2 = 3cm
+ Lại có: EI + IK + KF = EF
⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm

Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
=> EF là đường trung bình của hình thang ABCD
=> EF = (AB+DC)/2 = (8+12)/2 =10cm
Vậy EF = 10cm