Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

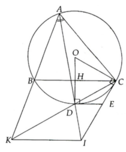
a, AD là phân giác B A C ^
=> D là điểm chính giữa B C ⏜ => OD ⊥ BC
Mà DE là tiếp tuyến => ĐPCM
b, E C D ^ = 1 2 s đ C D ⏜ = D A C ^ = B A D ^ => Đpcm
c, HC = P 3 2 => H O C ^ = 60 0 => B O C ^ = 120 0
=> l B C ⏜ = π . R . 120 0 180 0 = 2 3 πR

1. Ta có:
ED,EAED,EA là tiếp tuyến của (O)
→ED⊥OD,EA⊥OA⇒ˆADE=ˆOAE=90o→ED⊥OD,EA⊥OA⇒ADE^=OAE^=90o
EDOAEDOA có ˆADE+ˆOAE=180oADE^+OAE^=180o
⇒EDOA⇒EDOA nội tiếp đường tròn đường kính (OE)
→ˆDOA+ˆDEA=180o→DOA^+DEA^=180o
Mà ABCDABCD là hình thang cân
→ˆDMA=ˆDBA+ˆCAB=2ˆDBA=ˆDOA→DMA^=DBA^+CAB^=2DBA^=DOA^
→ˆDMA+ˆAED=180o→AEDM→DMA^+AED^=180o→AEDM nội tiếp được trong một đường tròn
2. Từ câu 1
→ˆEMA=ˆEDA=ˆDBA=ˆCAB→EMA^=EDA^=DBA^=CAB^
Vì EDED là tiếp tuyến của (O),ABCDABCD là hình thang cân
→EM//AB→EM//AB
3. Ta có:
EM//AB→HK//AB→HMAB=DMDB=CMCA=MKABEM//AB→HK//AB→HMAB=DMDB=CMCA=MKAB
→MH=MK→M→MH=MK→M là trung điểm HK

Lời giải:
a)
Ta có:
\(BC\parallel AD\Rightarrow \widehat{ICB}=\widehat{IDA}\) (hai góc đồng vị)
Tứ giác $ABCD$ nội tiếp nên \(\widehat{IBC}=\widehat{IDA}\)
\(\Rightarrow \widehat{ICB}=\widehat{IBC}\) \(\Rightarrow \triangle IBC\) cân tại $I$
Do đó \(\widehat{BID}=\widehat{BIC}=180^0-2\widehat{ICB}=180^0-2\widehat{IDA}\) (1)
Mặt khác theo tính chất hai tiếp tuyến cắt nhau suy ra \(BK=KD\Rightarrow \triangle BKD\) cân, suy ra \(\widehat{BKD}=180^0-2\widehat{KDB}\) (2)
Vì \(\widehat{IBC}=\widehat{ICB}\) ta suy ra hai góc đồng vị tương ứng của nó cũng bằng nhau hay \(\widehat{IAD}=\widehat{IDA}\)
\(\Leftrightarrow \text{cung BD}=\text{cung AC}\Leftrightarrow \text{cung AB}=\text{cung CD}\)
Mà: \(\widehat{BDA}=\frac{1}{2}\text{cung AB}\); $DK$ là tiếp tuyến của (O) nên \(\widehat{CDK}=\frac{1}{2}\text{cung CD}\)
Suy ra \(\widehat{BDA}=\widehat{CDK}\Rightarrow \widehat{BDA}+\widehat{BDC}=\widehat{CDK}+\widehat{BDC}\)
hay \(\widehat{IDA}=\widehat{BDK}\) (3)
Từ (1); (2); (3) \(\Rightarrow \widehat{BID}=\widehat{BKD}\Rightarrow BIKD\) nội tiếp (đpcm)
b)
$BIKD$ nội tiếp \(\Rightarrow \widehat{KID}=\widehat{KBD}=\widehat{KDB}\)
Mà \(\widehat{KDB}=\widehat{IDA}\) (cmt) nên \(\widehat{KID}=\widehat{IDA}\). Hai góc này ở vị trí so le trong nên \(IK\parallel AD\parallel BC\)