Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Do I là trung điểm của DC nên ta có:
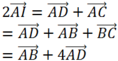
Lại có:
![]()
suy ra
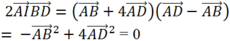
Vậy AI ⊥ BD.

Xét hình thang ADCB có
Q,P lần lượt là trung điểm của AB,DC
=>QP là đường trung bình của hình thang ADCB
=>QP//AD//BC và \(QP=\dfrac{AD+BC}{2}=\dfrac{\dfrac{BC}{2}+BC}{2}=\dfrac{3}{4}BC\)
Ta có: M là trung điểm của BC
=>\(BM=MC=\dfrac{BC}{2}\)
Ta có: N là trung điểm của MC
=>\(MN=NC=\dfrac{MC}{2}=\dfrac{BC}{4}\)
BM+MN=BN
=>\(BN=\dfrac{1}{4}BC+\dfrac{1}{2}BC=\dfrac{3}{4}BC\)
=>QP=BN
Ta có: QP//BN
QP=BN
Do đó: \(\overrightarrow{QP}=\overrightarrow{BN}\)
=>Điểm E trùng với điểm P

\(\overrightarrow{AB}.\overrightarrow{CD}=\overrightarrow{AB}\left(\overrightarrow{CB}+\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AB}.\overrightarrow{CB}+\overrightarrow{AB}.\overrightarrow{BA}+\overrightarrow{AB}.\overrightarrow{AD}\)
\(=0-\overrightarrow{AB}^2+0=-4a^2\)

Chọn D.
Phương án A: ![]() = AB.DC.cos00
= AB.DC.cos00
= 8a2 nên loại A.
Phương án B: ![]() suy ra
suy ra ![]() nên loại B.
nên loại B.
Phương án C: ![]() suy ra
suy ra ![]() nên loại C.
nên loại C.
Phương án D: ![]() không vuông góc với
không vuông góc với ![]() suy ra
suy ra ![]() nên chọn D.
nên chọn D.

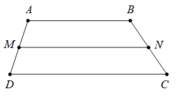
Vì M; N lần lượt là trung điểm của AD; BC
M A → + M D → = 0 → B N → + C N → = 0 → .
Dựa vào đáp án, ta có nhận xét sau:
A đúng, vì :
M D → + C N → + D C → = M N → = M D → + D C → + C N → = M C → + C N → = M N → .
B đúng, vì A B → − M D → + B N → = A B → + B N → − M D → = A N → − A M → = M N → .
C đúng, vì M N → = M A → + A B → + B N → và M N → = M D → + D C → + C N → .
Suy ra
2 M N → = M A → + M D → + A B → + D C → + B N → + C N → = 0 → + A B → + D C → + 0 → = A B → + D C →
⇒ M N → = 1 2 A D → + B C → .
D sai, vì theo phân tích ở đáp án C.
Chọn D.
Xét ΔADB có
\(cosA=\dfrac{AB^2+AD^2-DB^2}{2\cdot AB\cdot AD}\)
=>\(\dfrac{a^2+9a^2-DB^2}{2\cdot a\cdot3a}=\dfrac{1}{2}\)
=>\(10a^2-DB^2=3a^2\)
=>\(DB=a\sqrt{7}\)
Xét ΔABD có
\(cosABD=\dfrac{BA^2+BD^2-AD^2}{2\cdot BA\cdot BD}\)
\(=\dfrac{9a^2+7a^2-a^2}{2\cdot3a\cdot a\sqrt{7}}=\dfrac{15a^2}{6a^2\cdot\sqrt{7}}=\dfrac{15}{6\sqrt{7}}=\dfrac{5}{2\sqrt{7}}\)
=>\(cosCDB=\dfrac{5}{2\sqrt{7}}\)(do \(\widehat{ABD}=\widehat{CDB}\) vì AB//CD)
Xét ΔCDB có \(cosCDB=\dfrac{DB^2+DC^2-BC^2}{2\cdot DB\cdot DC}\)
=>\(\dfrac{5}{2\sqrt{7}}=\dfrac{7a^2+a^2-BC^2}{2\cdot a\sqrt{7}\cdot a}\)
=>\(\dfrac{8a^2-BC^2}{2a^2\sqrt{7}}=\dfrac{5}{2\sqrt{7}}\)
=>\(\dfrac{8a^2-BC^2}{a^2}=5\)
=>\(8a^2-BC^2=5a^2\)
=>\(BC^2=3a^2\)
=>\(BC=a\sqrt{3}\)