Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*SABC=1/3SABCD(Vì có đáy = đáy bé và có chiều cao=chiều cao hình thang ABCD)
=>SABCD=24x3=72 cm2
Đáp số: 72 cm2

Diện tích hình tam giác DOC là:
\(\text{128 : 4 × 3= 48 ( cm )}\)
Đáp số :\(\text{ 48cm}\)

Bài này m dùng định lý Ta-lét đc nhưng đây là toán lớp 5 thật à"?
oa toán hình lp 5 này của bn khó quá ha, hồi mình hok lp 5 đâu có mấy kiểu này nhỉ ^^

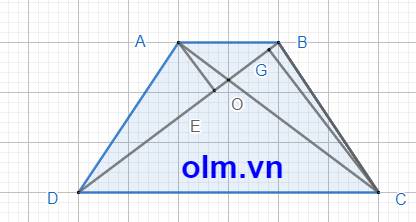
a, Dựng chiều cao CG của \(\Delta\)BCD và chiều cao AE của \(\Delta\) ABD
\(\dfrac{S_{ABD}}{S_{BCD}}\) = \(\dfrac{AE}{CG}\) (vì hai tam giác có chung cạnh đáy BD nên tỉ số diện tích là tỉ số hai chiều cao tương ứng)
\(\dfrac{S_{ABD}}{S_{BCD}}\) = \(\dfrac{AB}{CD}\) (vì hai tam giác có chiều cao bằng nhau nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy)
⇒ \(\dfrac{AE}{CG}\) = \(\dfrac{AB}{CD}\) = \(\dfrac{1}{3}\)
\(\dfrac{S_{AOB}}{S_{BOC}}\) = \(\dfrac{AE}{CG}\) ( hai tam giác có chung cạnh đáy OB nên tỉ số diện tích là tỉ số hai chiều cao tương ứng)
\(\dfrac{S_{AOB}}{S_{BOC}}\) = \(\dfrac{AO}{OC}\) ( vì hai tam giác có chiều cao bằng nhau nên tỉ số diện tích là tỉ số hai cạnh đáy)
⇒ \(\dfrac{AE}{CG}\) = \(\dfrac{AO}{OC}\) = \(\dfrac{1}{3}\)
Chứng minh tương tự ta có: \(\dfrac{BO}{OD}\) = \(\dfrac{1}{3}\)
b, SABD = SABC ( vì hai tam giác có chung cạnh đáy AB và hai chiều cao bằng nhau)
SABD = SABO + SAOD = SAOB + SBOC = SABC
SAOD \(\times\) 1 = SBOC
SAOD \(\times\) 1 = SAOD
SAOD \(\times\) \(\dfrac{1}{3}\) = SAOB (vì hai tam giác có chung chiều cao hạ từ đỉnh A xuống đáy BD và \(\dfrac{OB}{OD}\) = \(\dfrac{1}{3}\))
SAOD \(\times\) 3 = SDOC ( vì hai tam giác có chung chiều cao hạ từ đỉnh D xuống đáy AC và \(\dfrac{AO}{OC}\) =\(\dfrac{1}{3}\))
Cộng các vế trên ta với nhau ta có diện tích hình thang ABCD bằng:
1 + 1 + \(\dfrac{1}{3}\) + 3 = \(\dfrac{16}{3}\) ( diện tích hình tam giác AOD)
Diện tích tam giác AOD là: 32 : \(\dfrac{16}{3}\) = 6 (m2)
ĐS...
Mọi ng giải nhanh giúp mình nhé, mình đag cần gấp lắm, mai đi học r, cảm ơn mng nh🥹