Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D M N P Q
+) Hình thang ABCD có M; N là trung điểm của AD; BC => MN là đường trung bình của hình thang
=> MN // AB // CD và MN = (AB + CD)/2
+) Tam giác ADB có MP // AB; M là trung điểm của AD => P là trung điểm của DB
Tam giác ABC có NQ // AB; N là trung điểm của BC => Q là trung điểm của AC
+) 2.MN = AB + CD => AB = 2.MN - CD = 2.6 - 8 = 4 cm
c) MP = AB/2 = 4/2 = 2 cm
QN = AB/2 = 4/2 = 2 cm
=> PQ = MN - MP - QN = 6 - 2 - 2 = 2 cm
ĐS:...
Chỉ hình thang ABCD (AB//CD). Phân giác góc A cắt BC tại E.
a) CM: AB=BE
b) Phân giác góc B cắt AE tại F. CMR: BF vuông góc với AE và FA.FE.
c) Gọi M,N lần lượt là trung điểm cua AB và CD. CMR: M,F,N thẳng hàng

???????????????????????????????????!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!?????????????????????????????????????????????????????????????????????????????????????

Áp dụng đường trung bình là xong
a, Hình thang ABCD có: \(AM=MD\left(gt\right)\)
\(AN=NC\left(gt\right)\)
\(\Rightarrow\)MN là đường trung bình của hình thang ABCD \(\Rightarrow\hept{\begin{cases}MN//AB//CD\\MN=\frac{AB+CD}{2}\end{cases}\Leftrightarrow6=\frac{AB+8}{2}\Leftrightarrow AB=4\left(cm\right)}\)
b, \(\Delta ABD\)có: \(MP//AB\left(cmt\right)\)
\(AM=MD\left(gt\right)\)
\(\Rightarrow DP=PB\)
\(\Delta ABD\)có: \(AM=MD\left(gt\right)\)
\(DP=PB\left(cmt\right)\)
\(\Rightarrow\)MP là đường trung bình của \(\Delta ABD\Rightarrow MP=\frac{1}{2}AB\Leftrightarrow MP=\frac{1}{2}.4=2\left(cm\right)\)
Chứng minh tương tự ta có: \(QN=2\left(cm\right)\)
Ta có: \(MP+PQ+QN=MN\Leftrightarrow2+PQ+2=6\Leftrightarrow PQ=2\left(cm\right)\)
Cơ mà thấy câu b cứ thấy nó cứ sao sao á, nếu sai thì báo nhá.

a/
△ACD có:
- MN lần lượt đi qua trung điểm của AD và AC tại M và N
=> MN là đường trung bình của △ACD
Mặt khác, hình thang ABCD có:
- MP lần lượt đi qua trung điểm của AD và BC tại M và P
=> MP là đường trung bình của hình thang ABCD
=> MN trùng MP
Vậy: M, N, P thẳng hàng. (đpcm)
b/
- MN là đường trung bình của △ACD (cmt)
=> \(MN=\dfrac{1}{2}CD\)
Hay: \(MN=\dfrac{1}{2}.7=3,5\left(cm\right)\)
- MP là đường trung bình của hình thang ABCD (cmt)
=> \(MP=\dfrac{1}{2}AB.CD\)
Hay: \(MP=\dfrac{5+7}{2}=6\left(cm\right)\)
- \(NP=MP-MN\)
Hay: \(NP=6-3,5=2,5\left(cm\right)\)
- Nhận xét: Độ dài MP = 1/2 tổng độ dài hai đáy AB và CD
Vậy:
\(MN=3,5\left(cm\right)\)
\(NP=2,5\left(cm\right)\)
\(MP=6\left(cm\right)\)
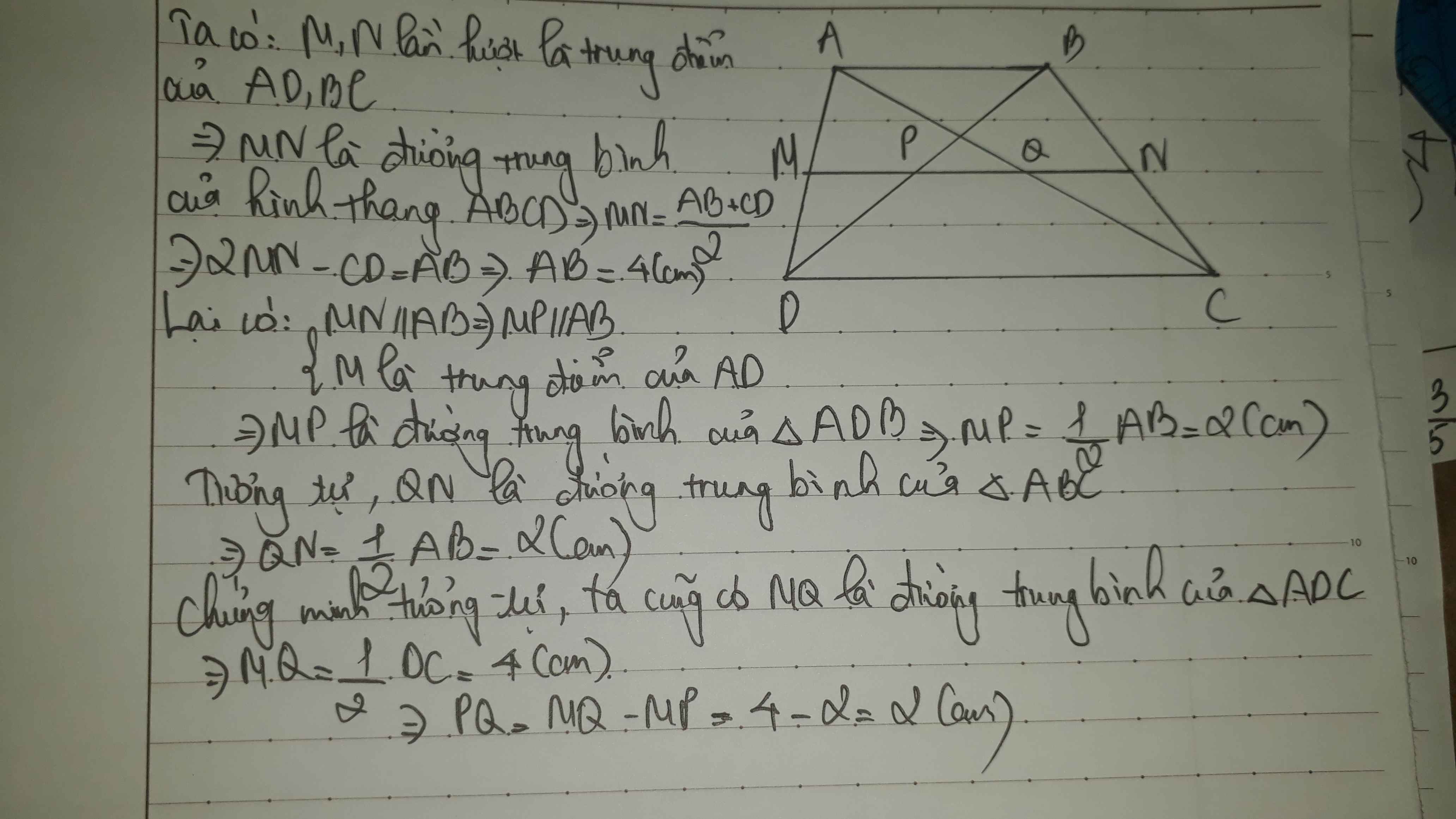
A B D E F C I K M
em cần lời giải ạ