Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
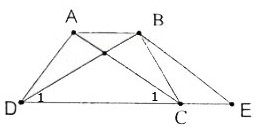
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra 
= 
(3)
∆BDE cân tại B (câu a) nên 
= (4)
Từ (3) và (4) suy ra =
Xét ∆ACD và ∆BCD có AC = BD (gt)
= (cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra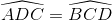 
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra = (3)
∆BDE cân tại B (câu a) nên = (4)
Từ (3) và (4) suy ra =
Xét ∆ACD và ∆BCD có AC = BD (gt)
= (cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra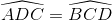
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
A B C D O 1 2 1 2 1 2
1. Xét tam giác ABD và tam giác ABC có:
AB chung
AD=BC ( ABCD là hình thang cân)
\(\widehat{A}=\widehat{B}\)( hai góc đối đỉnh)
=> Tam giác ABD= Tam giác ABC
2.
Ta có: Tam giác ABD= Tam giác ABC ( theo câu 1)
=> \(\widehat{A_1}=\widehat{B_2}\)
=> Tam giác OAB cân
=> OA=OB
3.
Ta có \(\widehat{D}=\widehat{C}\)( ABCD là hình thang cân)
=> \(\widehat{D_1}+\widehat{D_2}=\widehat{C_1}+\widehat{C_2}\)
Mà \(\widehat{D_1}=\widehat{C_1}\)( Tam giác ABD= Tam giác ABC)
=> \(\widehat{D_2}=\widehat{C_2}\)
=> Tam giác DOC cân tại O
=> DO=CO
Bài toán 8 mà sao giống toán 7 thế nhỉ?
A B C D O
a) Trong hình thang câng hai cạnh bên bằng nhau (AD = BC)
Hai góc kề ở 1 đáy bằng nhau nên theo tính chất hai đoạn thẳng song song suy ra hai góc kề ở đáy kia cũng bằng nhau.
Suy ra \(\widehat{A}=\widehat{B};\widehat{C}=\widehat{D}\)
Xét tam giác ABD và tam giác BAC có:
AD = BC (gt)
\(\widehat{A}=\widehat{B}\)
\(AB:\text{ cạnh chung }\)
\(\Rightarrow\Delta ABD=\Delta BAC\)
b) Do \(\Delta ABD=\Delta BAC\Rightarrow\widehat{DBA}=\widehat{BAC}\left(\text{hai góc tương ứng}\right)\)
\(\Rightarrow\Delta OAB\text{ cân tại O }\Rightarrow OA=OB\) (theo tính chất tam giác cân)
c) Cũng do \(\Delta ABD=\Delta BAC\Rightarrow BD=AC\Leftrightarrow OB+OD=OA+OC\)
Theo kết quả câu b ta có OA = OB suy ra OD = OC (đpcm)
a: Ta có: AB//CD
=>\(\hat{OAB}=\hat{ODC}\) (hai góc đồng vị) và \(\hat{OBA}=\hat{OCD}\) (hai góc đồng vị)
mà \(\hat{ODC}=\hat{OCD}\)
nên \(\hat{OAB}=\hat{OBA}\)
=>ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ΔABD=ΔBAC
=>\(\hat{ABD}=\hat{BAC}\)
=>\(\hat{EAB}=\hat{EBA}\)
=>EA=EB
Ta có: EA+EC=AC
EB+ED=BD
mà EA=EB và AC=BD
nên EC=ED
d: Ta có: OA+AD=OD
OB+BC=OC
mà AO=OB và AD=BC
nên OD=OC
=>O nằm trên đường trung trực của DC(1)
Ta có: EC=ED
=>E nằm trên đường trung trực của CD(2)
Từ (1),(2) suy ra OE là đường trung trực của CD
=>OE đi qua trung điểm của CD
=>O,E,trung điểm của CD thẳng hàng
Bài 1:
A B C D O M N P Q
a) Xét tam giác AOD có M là trung điểm của AO (gt) Q là trung điểm của OD (gt)
\(\Rightarrow MQ//AD,MQ=\frac{1}{2}AD\left(tc\right)\left(1\right)\)
CMTT \(MN//AB,MN=\frac{1}{2}AB\left(2\right)\)
\(NP=\frac{1}{2}BC\left(3\right)\)
\(PQ=\frac{1}{2}DC\left(4\right)\)
Mà AB=BC=CD=DA (tc) (5)
Từ (1) ,(2) ,(3),(4) và (5)\(\Rightarrow MN=NP=PQ=MQ\)
Xét tứ giác MNPQ có \(MN=NP=PQ=MQ\left(gt\right)\)
\(\Rightarrow MNPQ\)là hình thoi ( dhnb) (6)
Ta có: \(\hept{\begin{cases}MQ//AD\left(cmt\right)\\MN//AB\left(cmt\right)\end{cases}}\)mà \(AD\perp AB\)
\(\Rightarrow MQ\perp MN\)
\(\Rightarrow\widehat{QMN}=90^0\)(7)
Từ (6) và (7) \(\Rightarrow MNPQ\)là hình vuông (dhnb )
b) Ta có\(MQ=\frac{1}{2}AD\left(cmt\right)\)
mà \(AD=16\left(cm\right)\)
\(\Rightarrow MQ=8\left(cm\right)\)
\(\Rightarrow S_{MNPQ}=8^2=64\left(cm^2\right)\)
\(\Rightarrow S_{ABCD}=16^2=256\left(cm^2\right)\)
Vậy diện tích phần trong của hình vuông ABCD nằm ngoài tứ giác MNPQ =\(256-64=192\left(cm^2\right)\)
A B D C O K H
Kẻ \(BH\perp AD,CK\perp AD\)
\(\Rightarrow BH//CK\)
Ta có: \(\hept{\begin{cases}BH//CK\\BC//HK\end{cases}\Rightarrow BH=CK}\)( tc cặp đoạn chắn )
Xét tam giác ABD và tam giác ACD có:
2 đường cao BH,CK = nhau , đáy AD chung
\(\Rightarrow S_{ABD}=S_{ACD}\)
\(\Leftrightarrow S_{OAB}+S_{AOD}=S_{AOD}+S_{OCD}\)
\(\Leftrightarrow S_{OAB}=S_{OCD}\left(đpcm\right)\)
PS: có 1 tính chất học ở kì I lớp 8 á nhưng mình không biết cách giải thích sao nữa nên mình dùng cặp đoạn chắn
Sửa đề: ABCD là hình thang cân
a: AB//CD
=>\(\hat{OAB}=\hat{ADC}\) (hai góc đồng vị) và \(\hat{OBA}=\hat{BCD}\) (hai góc đồng vị)
mà \(\hat{ADC}=\hat{BCD}\) (ABCD là hinh thang cân)
nên \(\hat{OAB}=\hat{OBA}\)
=>ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔBAD=ΔABC
A B E C D 1 1
a) Hình thang ABEC ( AB // CE ) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\)cân
b) Do AC // BE nên \(\widehat{E}=\widehat{C_1}\left(3\right)\)
Mà tam giác BDE cân tại B ( câu a ) nên \(\widehat{E}=\widehat{D_1}\left(4\right)\)
Từ (3)(4) => \(\widehat{D_1}=\widehat{C_1}\)
* Xét 2 tam giác : ACD và BDC có :
DC chung
AC = BD ( gt )
\(\widehat{C_1}=\widehat{D_1}\left(cmt\right)\)
\(\Rightarrow\Delta ACD=\Delta BDC\left(c-g-c\right)\)
c) Theo ( c/m câu b ) ta có :
\(\Delta ACD=\Delta BDC\)
nên \(\widehat{ADC}=\widehat{BCD}\)( 2 góc tương ứng )
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
a: Xét ΔDAC và ΔCBD có
DA=BC
AC=BD
DC chung
Do đó: ΔDAC=ΔCBD
=>\(\hat{DAC}=\hat{CBD}\)
=>\(\hat{DAC}=90^0\)
=>AD⊥ AC
b: ABCD là hình thang cân
=>AD=BC
mà AB=BC
nên AD=AB=BC
Ta có: AD=AB
=>ΔABD cân tại A
=>\(\hat{ABD}=\hat{ADB}\)
mà \(\hat{ABD}=\hat{BDC}\) (hai góc so le trong, AB//DC)
nên \(\hat{ADB}=\hat{CDB}\)
=>DB là phân giác của góc ADC
=>\(\hat{ADC}=2\cdot\hat{BDC}\)
Ta có: BA=BC
=>ΔBAC cân tại B
=>\(\hat{BAC}=\hat{BCA}\)
mà \(\hat{BAC}=\hat{ACD}\) (hai góc so le trong, AB//CD)
nên \(\hat{BCA}=\hat{DCA}\)
=>CA là phân giác của góc BCD
=>\(\hat{BCD}=2\cdot\hat{ACD}\)
ΔADC=ΔBCD
=>\(\hat{ACD}=\hat{BDC}\)
=>\(\hat{BDC}=\frac12\cdot\hat{BCD}\)
ΔBDC vuông tại B
=>\(\hat{BDC}+\hat{BCD}=90^0\)
=>\(\frac12\cdot\hat{BCD}+\hat{BCD}=90^0\)
=>\(1,5\cdot\hat{BCD}=90^0\)
=>\(\hat{BCD}=60^0\)
=>\(\hat{ADC}=\hat{BCD}=60^0\)
AB//CD
=>\(\hat{ABC}+\hat{BCD}=180^0\)
=>\(\hat{ABC}=180^0-60^0=120^0\)
ABCD là hình thang cân
=>\(\hat{BAD}=\hat{ABC}\)
=>\(\hat{BAD}=120^0\)
c: Kẻ OK⊥AD tại K; OE⊥DC tại E; OH⊥BC tại H
=>OK,OE,OH lần lượt là khoảng cách từ O xuống AD,DC,BC
Xét ΔDKO vuông tại K và ΔDEO vuông tại E có
DO chung
\(\hat{KDO}=\hat{EDO}\)
Do đó: ΔDKO=ΔDEO
=>OK=OE
Xét ΔCEO vuông tại E và ΔCHO vuông tại H có
CO chung
\(\hat{ECO}=\hat{HCO}\)
Do đó: ΔCEO=ΔCHO
=>OE=OH
=>OE=OH=OK
=>O cách đều hai cạnh bên và đáy lớn của hình thang cân ABCD
a: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: ˆACD=ˆBDCACD^=BDC^
hay ˆODC=ˆOCDODC^=OCD^
Xét ΔOCD có ˆODC=ˆOCDODC^=OCD^
nên ΔOCD cân tại O
Suy ra: OC=OD
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB
* Ta có: OA = OB nên tam giác OAB cân tại O
* Do OC = OD nên tam giác OCD cân tại O
* vì OA = OB và OC = OD nên OA + OC = OB + OD
Hay AC = BD
Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.
Suy ra: BC = AD và B A D ^ = A B C ^ ; A D C ^ = D C B ^
Chọn đáp án D