Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hthang ABCD có:
M là trung điểm AD(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
\(\Rightarrow MN=\dfrac{AB+CD}{2}\)
\(\Rightarrow AB=2MN-CD\)
\(\Rightarrow AB=2.3-4=2\left(cm\right)\)

Tam giác AHD vuông tại H có HM là đường trung tuyến ứng với cạnh huyền AD
\(\Rightarrow HM=MD=\frac{1}{2}AD\)
\(\Rightarrow\Delta HMD\)cân tại M \(\Rightarrow\widehat{D}=\widehat{MHD}\)
Mà \(\widehat{D}=\widehat{C}\left(gt\right)\Rightarrow\widehat{MHD}=\widehat{C}\Rightarrow MH//NC\)
Mặt khác, \(HM=\frac{1}{2}AD=\frac{1}{2}BC=NC\)
Tứ giác MNHC có: MH // NC và MH = NC
Do đó: MHCN là hình bình hành (DHNB) \(\Rightarrow MN=HC=5cm\)

Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC.
Suy ra, MN là đường trung bình của hình thang
Do đó:
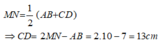
Chọn đáp án D

a) Xét tam giác ABD có :
M là trung điểm của AB
F là trung điểm của BD
=) MF là đường trung bình của tam giác ABD
=) MF//AD và MF=\(\frac{1}{2}\)AD (1)
Xét tam giác tam giác ACD có :
N là trung điểm CD
E là trung điểm AC
=) NE là đường trung bình của tam giác ACD
=) NE//AD và NE=\(\frac{1}{2}\)AD (2)
Từ (1) và (2) =) Tứ giác MENF là hình bình hành

Xét hthang ABCD có:
M là trung điểm AD(gt)
N là trung điểm BC(gt)
=> MN là đường trung bình
\(\Rightarrow MN=\dfrac{AB+CD}{2}\left(t/c\right)\)
\(\Rightarrow AB=2MN-CD=2.3-4=2\left(cm\right)\)

Xét hình thang ABCD có:
\(MA=MB\left(gt\right)\)
\(NB=NC\left(gt\right)\)
\(\Rightarrow\)MN là đường trung bình của hình thang ABCD
\(\Rightarrow\)\(MN=\frac{AB+CD}{2}\)( định lý 4 về đường trung bình của hình thang )
Hay \(28=\frac{AB+CD}{2}\)
\(\Rightarrow AB+CD=28\cdot2=56\)
Mặt khác ta có: \(\frac{AB}{CD}=\frac{3}{5}\left(gt\right)\)
Hay: \(\frac{AB}{3}=\frac{CD}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{AB}{3}=\frac{CD}{5}=\frac{AB+CD}{3+5}=\frac{56}{8}=7\)
\(\Rightarrow\orbr{\begin{cases}AB=7\cdot3=21\\CD=7\cdot5=35\end{cases}}\)
Vậy: \(AB=21cm\)
\(CD=35cm\)
hình như bạn cho cái đề thiếu BC nhỉ!