Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2. A B C D O E F
+ AB // CD \(\Rightarrow\dfrac{AO}{CO}=\dfrac{BO}{DO}\)
\(\Rightarrow\dfrac{AO}{AO+CO}=\dfrac{BO}{BO+DO}\Rightarrow\dfrac{AO}{AC}=\dfrac{BO}{BD}\)
+ OE // CD => \(\dfrac{OE}{CD}=\dfrac{AO}{AC}\)
+ OF // CD => \(\dfrac{OF}{DC}=\dfrac{BO}{BD}\)
\(\Rightarrow\dfrac{OE}{CD}=\dfrac{OF}{DC}\Rightarrow OE=OF\)
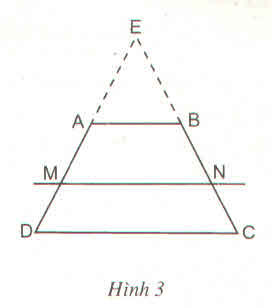
Bài 1:
a: Xét hình thang ABCD có MN//AB//CD
nên AM/MD=BN/NC
b: AM/MD=BN/NC
=>MD/AM=NC/BN
=>\(\dfrac{MD+AM}{AM}=\dfrac{NC+BN}{BN}\)
=>AD/AM=BC/BN
=>AM/AD=BN/BC
c: AM/AD=BN/BC
=>1-AM/AD=1-BN/BC
=>DM/AD=CN/CB

Giải:
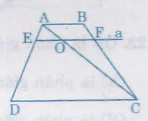
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF

Lời giải:
$AB,BC,AC$ tỉ lệ với $4,7,5$ \(\Leftrightarrow \frac{AB}{4}=\frac{BC}{7}=\frac{CA}{5}(*)\)
a) Sử dụng công thức đường phân giác kết hợp với \((*)\) ta có:
\(\frac{MC}{BM}=\frac{AC}{AB}=\frac{5}{4}\)
\(\Rightarrow \frac{MC}{BM+MC}=\frac{5}{4+5}\Leftrightarrow \frac{MC}{BC}=\frac{5}{9}\)
\(\Rightarrow MC=\frac{5}{9}BC=\frac{5}{9}.18=10\) (cm)
b) Sử dụng công thức đường phân giác kết hợp với \((*)\) ta có:
\(\frac{NC}{NA}=\frac{BC}{AB}=\frac{7}{4}\)\(\Leftrightarrow \frac{NC}{7}=\frac{NA}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{NC+NA}{7+4}=\frac{NC}{7}=\frac{NA}{4}=\frac{NC-NA}{7-4}\)
\(\Leftrightarrow \frac{AC}{11}=\frac{3}{3}=1\Rightarrow AC=11\) (cm)
c)
Vì $AO$ là phân giác góc $PAC$, $BO$ là phân giác góc $PBC$ nên áp dụng công thức đường phân giác:
\(\frac{OP}{OC}=\frac{AP}{AC}=\frac{BP}{BC}\)
AD tính chất dãy tỉ số bằng nhau:
\(\frac{OP}{OC}=\frac{AP}{AC}=\frac{BP}{BC}=\frac{AP+BP}{AC+BC}=\frac{AB}{AC+BC}\)
Theo \((*)\Rightarrow AC=\frac{5}{4}AB; BC=\frac{7}{4}AB\)
\(\frac{OP}{OC}=\frac{AB}{AC+BC}=\frac{AB}{\frac{5}{4}AB+\frac{7}{4}AB}=\frac{AB}{3AB}=\frac{1}{3}\)
d) Áp dụng công thức đường phân giác:
\(\left\{\begin{matrix} \frac{MB}{MC}=\frac{AB}{AC}\\ \frac{NC}{NA}=\frac{BC}{AB}\\ \frac{PA}{PB}=\frac{AC}{BC}\end{matrix}\right.\Rightarrow \frac{MB}{MC}.\frac{NC}{NA}.\frac{PA}{PB}=\frac{AB}{AC}.\frac{BC}{AB}.\frac{AC}{BC}=1\)
(đpcm)
Chứng minh \(\frac{1}{AM}+\frac{1}{BN}+\frac{1}{CP}>\frac{1}{AB}+\frac{1}{BC}+\frac{1}{AC}\)
Kẻ \(MH\perp AB, MK\perp AC, CL\perp AB\)
Ta có bổ đề sau: \(\sin (2\alpha)=2\sin \alpha\cos \alpha\)
Chứng minh :
Thật vậy, xét một tam giác $ABC$ vuông tại $A$ có đường cao $AH$ và trung tuyến $AM$, góc \(\angle ACB=\alpha\)
Khi đó: \(AM=MB=MC=\frac{BC}{2}\Rightarrow \triangle AMC\) cân tại $M$
\(\Rightarrow \angle MAC=\angle MCA=\alpha\)
\(\Rightarrow \angle HMA=\angle MAC+\angle MCA=2\alpha\)
\(\Rightarrow \sin 2\alpha=\sin HMA=\frac{HA}{MA}=\frac{HA}{\frac{BC}{2}}=\frac{2HA}{BC}\) (1)
Lại có: \(\sin \alpha=\sin \angle ACB=\frac{AH}{AC}\)
\(\cos \alpha=\frac{AC}{BC}\)
\(\Rightarrow \sin \alpha\cos \alpha=\frac{AH}{AC}.\frac{AC}{BC}=\frac{AH}{BC}\) (2)
Từ (1); (2) suy ra \(\sin 2\alpha=2\sin \alpha\cos \alpha\) (đpcm)
------------------------------
Áp dụng vào bài toán:
Ta có: \(\sin A=2\sin \frac{A}{2}\cos \frac{A}{2}\)
\(S_{ABM}+S_{AMC}=S_{ABC}\)
\(\Leftrightarrow \frac{MH.AB}{2}+\frac{MK.AC}{2}=\frac{CL.AB}{2}\)
\(\Leftrightarrow AB.\sin \frac{A}{2}.AM+\sin \frac{A}{2}.AM.AC=\sin A.AC.AB\)
\(\Leftrightarrow AM=\frac{\sin A.AB.AC}{\sin \frac{A}{2}.AB+\sin \frac{A}{2}.AC}=\frac{2\sin \frac{A}{2}\cos \frac{A}{2}.AB.AC}{\sin \frac{A}{2}.AB+\sin \frac{A}{2}.AC}\)
\(\Leftrightarrow AM=\frac{2\cos \frac{A}{2}.AB.AC}{AB+AC}\)
\(\Leftrightarrow \frac{1}{AM}=\frac{AB+AC}{2AB.AC\cos \frac{A}{2}}=\frac{1}{2\cos \frac{A}{2}}(\frac{1}{AB}+\frac{1}{AC})\)
Tương tự: \(\frac{1}{BN}=\frac{1}{2\cos \frac{B}{2}}(\frac{1}{BA}+\frac{1}{BC})\)
\(\frac{1}{CP}=\frac{1}{2\cos \frac{C}{2}}(\frac{1}{CB}+\frac{1}{CA})\)
Cộng theo vế:
\(\frac{1}{AM}+\frac{1}{BN}+\frac{1}{CP}=\frac{1}{2\cos \frac{A}{2}}(\frac{1}{AB}+\frac{1}{AC})+\frac{1}{2\cos \frac{B}{2}}(\frac{1}{BA}+\frac{1}{BC})+\frac{1}{2\cos \frac{C}{2}}(\frac{1}{CA}+\frac{1}{CB})\)
\(> \frac{1}{2}(\frac{1}{AB}+\frac{1}{AC})+\frac{1}{2}(\frac{1}{BC}+\frac{1}{AC})+\frac{1}{2}(\frac{1}{CB}+\frac{1}{CA})\) (do \(\cos \alpha < 1\) vì cạnh góc vuông luôn nhỏ hơn cạnh huyền)
\(\Leftrightarrow \frac{1}{AM}+\frac{1}{BN}+\frac{1}{CP}> \frac{1}{AB}+\frac{1}{BC}+\frac{1}{CA}\)
Ta có đpcm.

Xét hình thang ABCD có EF//AB//CD
nên AE/AD=BF/BC(1)
Xét ΔADC có EO//DC
nên EO/DC=AE/AD(2)
Xét ΔBDC có OF//DC
nên OF/DC=BF/BC(3)
Từ (1), (2) và (3) suy ra OE=OF