Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
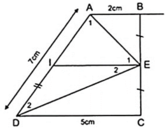
Do E là trung điểm của BC theo giả thiết vẽ I là trung điểm của AD thì
AI = ID = AD/2 = 3,5( cm ). ( 1 )
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có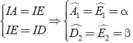
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có
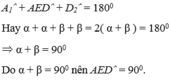
a, AD // BC (gt)
=> góc A + góc B = 180 (đl)
mà góc B = góc C do ABCD là hình thang cân (gt)
=> góc A + góc C = 180
Mà góc A = 60 (gt)
=> góc C = 180 - 60
=> góc C = 120
b. Có D; E lần lượt là trung điểm của AB; CD (gt)
=> DE là đường trung bình của hình thang ABCD (đn)
=> DE // BC // AD (đl)
có D là trung điểm của AB (gt)
=> O là trung điểm của AC (Đl)
=> OA = OC (đn)
c, có DE là đường trung bình của hình thang ABCD (câu b)
=> DE = (BC + AD) : 2 (Đl)
=> 2DE = BC + AD
=> 2DE - AD = BC
mà DE = 5 cm (gt)
AD = 7 cm (gT)
=> 2.5 - 7 = BC
=> BC = 3 (cm)
có D là trung điểm của AB (gt) ; O là trung điểm của AC (câu b)
=> DO là đường trung bình của tam giác ABC (đn)
=> OD = BC : 2 (đl) mà BC = 3 (cmt)
=> OD = 3 : 2
=> OD = 1,5
Ta có EI là đường trung bình của hình thang ABCD.
Áp dụng định lý đường trung bình của hình thang ABCD ta có:
IE = (AB + CD)/2 = (2 + 5)/2 = 3,5( cm ) ( 2 )
Từ ( 1 ) và ( 2 ) ta có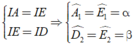
(vì trong tam giác, đối diện với hai cạn bằng nhau là hai góc bằng nhau)
+ Xét tam giác ADE có