Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: A D E ^ = 1 2 D ^ ngoài, D A E ^ = 1 2 A ^ ngoài.
Mà A ^ ngoài + D ^ ngoài = 1800 (do AB//CD)
⇒ A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), EF = 1 2 ( A B + B C + C D + D A )

a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: A D E ^ = 1 2 D ^ ngoài, D A E ^ = 1 2 A ^ ngoài.
Mà A ^ ngoài + D ^ ngoài = 1800 (do AB//CD)
⇒ A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), EF = 1 2 ( A B + B C + C D + D A )
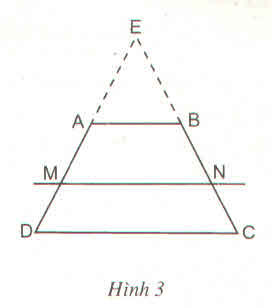
a:
góc AMD=180 độ-góc MAD-góc MDA
\(=180^0-\dfrac{180^0-\widehat{BAD}}{2}-\dfrac{180^0-\widehat{ADC}}{2}\)
\(=180^0-\dfrac{1}{2}\widehat{ADC}-90^0+\dfrac{1}{2}\widehat{ADC}=90^0\)
Gọi giao của AM với DC là M'
Xét ΔDM'A có
DM là đường cao, là đường phân giác
nên ΔDM'A cân tại D
=>M là trung điểm của AM'
Gọi giao của BN với DC là N'
Ta có: \(\widehat{BNC}=180^0-\widehat{NBC}-\widehat{NCB}\)
\(=180^0-\dfrac{180^0-\widehat{ABC}}{2}-\dfrac{180^0-\widehat{BCD}}{2}\)
\(=180^0-90^0+\dfrac{1}{2}\widehat{ABC}-90^0+\dfrac{1}{2}\widehat{BCD}\)
=90 độ
Xét ΔCN'B có
CN vừa là đường cao, vừa là phân giác
nên ΔCN'B cân tại C
=>N là trug điểm của BN'
Xét hình thang ABN'M' có
M,N lần lượt là trung điểm của AM' và BN'
nen MN là đường trung bình
=>MN//CD//AB
b: MN=(AB+M'N')/2
=(AB+M'D+CD+CN')/2
mà M'D=AD và CN'=CB
nên MN=(AB+CD+AD+CB)/2

A B E C D 1 1
a) Hình thang ABEC ( AB // CE ) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\)cân
b) Do AC // BE nên \(\widehat{E}=\widehat{C_1}\left(3\right)\)
Mà tam giác BDE cân tại B ( câu a ) nên \(\widehat{E}=\widehat{D_1}\left(4\right)\)
Từ (3)(4) => \(\widehat{D_1}=\widehat{C_1}\)
* Xét 2 tam giác : ACD và BDC có :
DC chung
AC = BD ( gt )
\(\widehat{C_1}=\widehat{D_1}\left(cmt\right)\)
\(\Rightarrow\Delta ACD=\Delta BDC\left(c-g-c\right)\)
c) Theo ( c/m câu b ) ta có :
\(\Delta ACD=\Delta BDC\)
nên \(\widehat{ADC}=\widehat{BCD}\)( 2 góc tương ứng )
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

Hướng dẫn cách vẽ hình : Cậu nên vẽ hình thang ABCD cân tại C và D và sao cho góc A và góc D là 2 góc kề 1 bên của tứ giác !!!!( ko bt vẽ trên này
Giải :
Ta có hình thang ABCD có 2 đáy AB và DC
=> AB//DC
Mà M là giao điểm phân giác của 2 góc B và góc D nằm trên AB
=> AM//DC
=> BM//DC
Vì AM//BC
=> AMD = MDC ( 2 góc so le trong ) ( 1)
Mà DM là pg ADC
=> ADM = MDC (2)
Từ (1) và (2) :
=> ADM = AMD
=> Tam giác AMD cân tại A
=> AD = AM(3)
Chứng minh tương tự ta cũng có tam giác MBC cân tại B và suy ra BC = MB(4)
Từ (3) và (4)
=> M là trung điểm AB
Còn ý b) ko bt làm
Sai thông cảm nhé

a) Xét tam giác ABC và tam giác BAD, ta có:
AB: cạnh chung
AC=AD (ABCD:hình thang cân)
BC=AD (ABCD: hình thang cân)
=>Tam giác ABC = tam giác BAD (c-c-c)
=>\(\widehat{ACB}\)=\(\widehat{BDA}\)(2 góc t/ứng)
Ta có:
\(\widehat{ACD=}\widehat{ACB}\)+\(\widehat{BCD}\)
BDC^ = BDA^ + ADC^
ACD^ = BDC^ (ABCD: hình thang cân)
ACB^ = BDA^ (cmt)
=>BCD^ = ADC^
Ta lại có AB//CD (gt):
=> ABC^ = BCD^ (2 góc sole trong)
BAD^ = ADC^ (2 góc sole trong)
BCD^ = ADC^ (cmt)
=> ABC^ = BAD^
Ta có ME//BC (gt):
=> MEA^ = ABC^ (2 góc sole trong)
Mà ABC^ = BAD^ (cmt)
=> MEA^ = BAD^
Mặt khác: MAE^ = BAD^ ( 2 góc đối đỉnh)
=> MEA^ = MAE^
=> Tam giác MAE cân tại M.
MIK xin lỗi, mik đánh sai đề bài, sửa lại như sau:
a) Tam giác MAE cân
b) AF = DE

Ko bt vẽ hình ở đây ntn Thông cảm 🙏🙏
Cách vẽ : Vẽ sao cho cân tại B và C và B ; C là 2 góc trong cùng phía , nối A với C
Giải:
a) Vì AB//DC ( gt)
=> BAC = ACD ( so le trong )
Mà AC là pg BCD
=> BCA = ACD
Mà BAC = ACD (cmt)
=> BCA = BAC
=> tam giác BAC cân tại B
B)
Giải :
Vì AH vuông góc với DC
=> BHD = 90 độ
Vì AF vuông góc với DC
=> AFC = 90 độ
=> AFC= BHD = 90 độ
=> AF// BH(1)
Vì AB// DC ( gt)
=> AB//FC (2)
Từ (1) và (2)=> AB = AF = FH = HB = 5cm ( Vì AF = 5cm) tính chất của hình thang
Vì tam giác ABC cân tại B ( cm ở ý a)
=> AB = BC = 5cm
Áp dụng định lý Py- ta - go ta có :
BC2= BG2+GC2
GC2=√25-- BG2
Tớ phân vân không biết đáp án của tớ có đúng không Nếu sai thông cảm nhé

Bài 1: Nhường chủ tus và các bạn:D
Bài 2(ko chắc nhưng vẫn làm:v): A B C D O
Do OA = OB(*) nên \(\Delta\)OAB cân tại O nên ^OAB = ^OBA (1)
Mặt khác cho AB // CD nên^OAB = ^OCD; ^OBA = ^ODC (so le trong) (2)
Từ (1) và (2) có ^OCD = ^ODC nên \(\Delta\) ODC cân tại O nên OC = OD (**)
Cộng theo vế (*) và (**) thu được:OA + OC = OB + OD
Hay AC = BD. Do đó hình thang ABCD có 2 đường chéo bằng nhau nên nó là hình thang cân (đpcm)

bạn tự vẽ hình nhé :)
a) ABCE là hình thang có 2 cạnh bên song song => AC=BE mà AC=BD => BE=BD => tam giác BDE cân tại B
b) tam giác BDE cân tại B => góc BDC=góc E mà góc ACD=góc E (2 góc đồng vị, AC//BE) => góc BDC= góc ACD
từ đó, chứng minh đc tg ACD=BDC (c-g-c)
c) tg ACD=BDC => góc ADC=góc BCD (2 góc tương ứng) => đpcm
tg BDE cân tại B:
ta có:ACD=BAC(AB//CD)
mà ACD =BEC =>BEC=BAC
xét tg ABC va tg ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
ma `BEC=ACD(đồng vị)
=>ACD=BDC
xét tg ACD va tg BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tg ACD = tg BDC
=>ADC=BCD
=>ABCD la hình thang cân (đpcm)



a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: A D E ^ = 1 2 D ^ ngoài, D A E ^ = 1 2 A ^ ngoài.
Mà A ^ ngoài + D ^ ngoài = 1800 (do AB//CD)
⇒ A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), EF = 1 2 ( A B + B C + C D + D A )
Lưu ý: Có thể sử dụng tính chất đường phân giác để chứng minh