K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
SG
Sách Giáo Khoa
28 tháng 4 2017

Cho hình thang ABCD (AB //CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14 cm. Tính độ dài MI, IK, KN ?
#Toán lớp 8
1
NT
Nguyen Thuy Hoa
29 tháng 6 2017

Đường trung bình của tam giác, hình thang

Đúng(1)
PT
Pham Trong Bach
14 tháng 7 2017

Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = l4cm. Tính độ dài MI, IK, KN.
#Toán lớp 8
1
CM
Cao Minh Tâm
14 tháng 7 2017

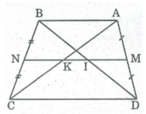
Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Hình thang ABCD có AB // CD

M là trung điểm của AD (gt)

N là trung điểm của BC (gt)

Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CD

MN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)

* Trong tam giác ADC, ta có:

M là trung điểm của AD

MK // CD

⇒ AK= KC và MK là đường trung bình của  ∆ ADC.

⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)

Vậy: KN = MN – MK = 10 – 7 = 3 (cm)

* Trong  ∆ ADB, ta có:

M là trung điểm của AD

MI // AB nên DI = IB

⇒ MI là đường trung bình của ∆ DAB

⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)

IK = MK – Ml = 7 – 3 = 4 (cm)

Đúng(1)
ML
Mã Lương Kim
14 tháng 9 2016 - olm

Cho hình thang ABCD (AB//CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I,K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB=6cm, CD = 14cm. Tính các độ dài MI,IK,KN.
#Toán lớp 8
0
HT
Huỳnh Thư Linh
10 tháng 9 2017 - olm

Cho hình thang ABCD (AB//CD), M là trung điểm của AD,N là trung điểm của BC. Gọi I,K theo thứ tự là giao điểm của MN với BD,AC. Cho biết AB=6cm CD=14cm. Tính các độ dài MI,IK,KN.
#Toán lớp 8
0
NT
Nguyễn Thị Quỳnh
17 tháng 7 2016 - olm

Cho hình thang ABCD (AB//CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I,K thao thứ tự là giao của MN với BD, AC. Cho biết AB=6cm, CD=14cm. Tính các độ dài MI, IK, KN.
#Toán lớp 8
0
NT
Nguyễn Thị Kim Anh
20 tháng 8 2017 - olm

Cho hình thang ABCD (AB//CD), M là trung điểm của AD ,N là trung điểm của BC .Gọi IK theo thứ tự là giao điểm của MN với BC, AC. Cho biết AB=6cm ,CD=14cm  Tính các độ dài MI,IK,KN
#Toán lớp 8
1
VT
Võ Thị Quỳnh Giang
21 tháng 8 2017

A B C D M N I K 6cm 14cm

xét hthang ABCD có: M là t/đ của AD(gt) , N là t/đ của BC(gt)

=> MN là đg trung bình của hthang ABCD=> MN//AB//CD và MN = 1/2 . (AB+CD)  (1)

xét tg ABD có: M là t/đ của AD(gt) , MI//AB (vì I thuộc MN , MN//AB) => I là t/đ của BD=>  MI là đg trung bình của tg ABD

=> MI=1/2.AB   => MI= 1/2.6=3(cm)   (vì AB=6 cm)

c/m tương tự ta đc: KN là đg trung bình của tg ABC =>   KN  =  1/2. AB  = 1/2.6  =3 (cm)  (vì AB =6cm)

Mặt khác : MN= MI +IK +KN  => MN=3 +IK +3 => MN= 6+ IK    (2)

Từ (1),(2) => 6+ IK = 1/2. (AB+CD)

   <=> 6+IK =1/2.(6+14)

<=> 6+ IK= 10

<=> IK =4  (cm)

Đúng(0)
HK
Huyền Khánh
8 tháng 11 2021
Câu 199. Cho hình thang ABCD ( AB / /CD) , M là trung điểm của AD , N là trung điểm của BC . Gọi I, K theo thứ tự là giao điêm của MN vớiMI , IK . BD, AC . Cho biết AB =6cm,CD =14cm . Tính độ dài A. MI = 4 cm, IK = 7cm .                                                      B.C. MI =3cm, IK = 7cm .                                                      ...
Đọc tiếp

Câu 199. Cho hình thang

 

ABCD ( AB / /CD) , M là trung điểm của AD ,

 

N là trung điểm của BC . Gọi

 

I, K theo thứ tự là giao điêm của MN với

MI , IK .

 

BD, AC . Cho biết AB =6cm,CD =14cm . Tính độ dài

 

A. MI = 4 cm, IK = 7cm .                                                      B.

C. MI =3cm, IK = 7cm .                                                       D.

 

MI = 4cm, IK =3cm .

MI =3cm, IK = 4cm .

 
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
8 tháng 11 2021

Chọn D

Đúng(0)
NT
Nguyễn Thiện Nhân
13 tháng 7 2017

Cho hình thang ABCD (AB //CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14 cm. Tính độ dài MI, IK, KN ?
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
21 tháng 5 2022

Xét hình thang ABCD có

M là trung điểm của AD

N là trung điểm của BC

Do đó: MN là đường trung bình

=>MN//AB//CD và \(MN=\dfrac{AB+CD}{2}=10\left(cm\right)\)

Xét ΔDAB có MI//AB

nên \(\dfrac{MI}{AB}=\dfrac{DM}{DA}\)

=>MI/6=1/2

hay MI=3(cm)

Xét ΔCAB có NK//AB

nên \(\dfrac{NK}{AB}=\dfrac{CN}{CB}\)

hay NK=3(cm)

=>IK=4(cm)

Đúng(0)
HN
hieu nguyen
16 tháng 9 2017 - olm

cho hình thang ABCD,M là trung điểm của AD,N là trung điểm của BC.gọi I,K theo thứ tự là giao điểm của MN với BD,AC.cho biết AB=6cm,CD=14cm.tính các độ độ dài MI,IK,KN.
#Toán lớp 8
2
HN
hieu nguyen
16 tháng 9 2017

vẽ hình cho đầy đủ nha!

Đúng(0)
OD
o0o_How dare you_o0o
27 tháng 8 2018

Cái gì mà khó vl

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP