
2. A B C D O E F
+ AB // CD \(\Rightarrow\dfrac{AO}{CO}=\dfrac{BO}{DO}\)
\(\Rightarrow\dfrac{AO}{AO+CO}=\dfrac{BO}{BO+DO}\Rightarrow\dfrac{AO}{AC}=\dfrac{BO}{BD}\)
+ OE // CD => \(\dfrac{OE}{CD}=\dfrac{AO}{AC}\)
+ OF // CD => \(\dfrac{OF}{DC}=\dfrac{BO}{BD}\)
\(\Rightarrow\dfrac{OE}{CD}=\dfrac{OF}{DC}\Rightarrow OE=OF\)
Bài 1:
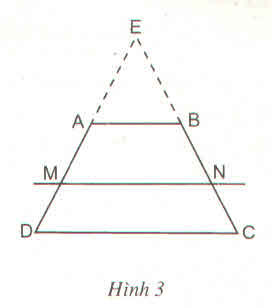
a: Xét hình thang ABCD có MN//AB//CD
nên AM/MD=BN/NC
b: AM/MD=BN/NC
=>MD/AM=NC/BN
=>\(\dfrac{MD+AM}{AM}=\dfrac{NC+BN}{BN}\)
=>AD/AM=BC/BN
=>AM/AD=BN/BC
c: AM/AD=BN/BC
=>1-AM/AD=1-BN/BC
=>DM/AD=CN/CB

A B C D E F I
Gọi I là giao điểm của BD và EF
EI//AB => \(\frac{DE}{AD}=\frac{ID}{DB}\)
IF//DC => \(\frac{BI}{BD}=\frac{BF}{BC}\)
=> \(\frac{DE}{AD}+\frac{BF}{BC}=\frac{ID}{DB}+\frac{BI}{BD}=\frac{BI+ID}{BD}=\frac{BD}{BD}=1\)
D C E I F A B
Gọi I là giao điểm của DB và EF
Xét tam giác ADB
Có : EI // AB
\(\Rightarrow\frac{DE}{AD}=\frac{ID}{DB}\)( 1 )
Xét tam giác DBC
Có : IF // DC
\(\Rightarrow\frac{BI}{BD}=\frac{BF}{BC}\)( 2 )
Từ (1)(2) , suy ra
\(\frac{DE}{AD}+\frac{BF}{BC}=\frac{ID}{DB}+\frac{BI}{BD}=\frac{BI+ID}{BD}=\frac{BD}{BD}=1\)
Vậy : \(\frac{ED}{AD}+\frac{BF}{BC}=1\)
Em làm kiểu này không biết có đúng không cô Chi check lại giúp em ạ <3

Nối A với C . Gọi O là giao điểm của AC và EF
Xét ΔADC có EO //DC
Áp dụng định lí Ta-lét cho ΔABC ta có :
\(\dfrac{ED}{AD}=\dfrac{OC}{AC}\left(1\right)\)
Xét ΔABC có OF //AB
Áp dụng định lí Ta -lét cho ΔABC :
\(\dfrac{BF}{BC}=\dfrac{AO}{AC}\left(2\right)\)
Từ (1) và (2) ta có : \(\dfrac{ED}{AC}+\dfrac{BF}{BC}=\dfrac{OC}{CA}+\dfrac{OA}{AC}=\dfrac{AC}{AC}=1\)
Vậy \(\dfrac{ED}{AD}+\dfrac{BF}{BC}=1\)



Giải:
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF