Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB\(\sim\)ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(2)
b: Xét ΔCAD có OE//AD
nên \(\dfrac{DE}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có OF//BC
nên \(\dfrac{CF}{CD}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{DE}{DC}=\dfrac{CF}{CD}\)
=>DE=CF

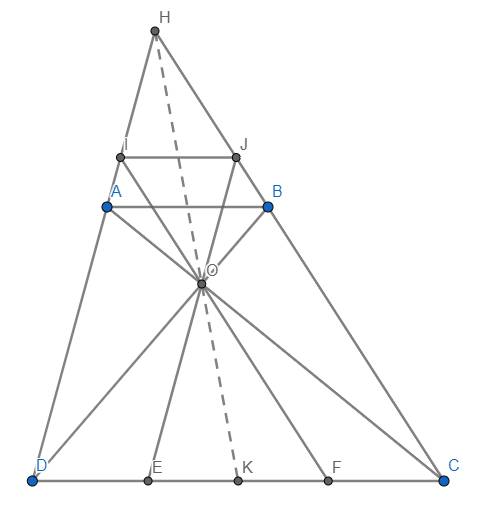
b) Theo Thales: \(\dfrac{DE}{DC}=\dfrac{AO}{AC};\dfrac{CF}{CD}=\dfrac{BO}{BD}\)
Theo câu a thì \(\dfrac{AO}{AC}=\dfrac{BO}{BD}\) \(\Rightarrow\dfrac{DE}{DC}=\dfrac{CF}{CD}\Rightarrow DE=CF\) (đpcm)
c) Từ \(DE=CF\Rightarrow\dfrac{DE}{EF}=\dfrac{CF}{EF}\)
Mà theo Thales: \(\dfrac{DE}{EF}=\dfrac{IO}{OF};\dfrac{CF}{EF}=\dfrac{JO}{OE}\)
Do đó \(\dfrac{IO}{OF}=\dfrac{JO}{OE}\) \(\Rightarrow\) IJ//CD//AB
d) Dùng định lý Menelaus đảo nhé bạn. Ta có \(\dfrac{HA}{HD}=\dfrac{AB}{CD}=\dfrac{OA}{OC}\) nê \(\dfrac{HA}{AD}.\dfrac{OC}{OA}=1\). Do K là trung điểm EF mà \(DE=CF\) nên K cũng là trung điểm CD hay \(\dfrac{KD}{KC}=1\). Do đó \(\dfrac{HA}{AD}.\dfrac{KD}{KC}.\dfrac{OC}{OA}=1\). Theo định lý Menalaus đảo \(\Rightarrow\)H, O, K thẳng hàng (đpcm)

a ) Vì \(\hept{\begin{cases}EA=ED\left(gt\right)\\FB=FC\left(gt\right)\end{cases}}\)
\(\Rightarrow\) EF là đường trung bình của hình thang ABCD.
\(\Rightarrow\) EF // AB // CD
Xét \(\Delta ABC\) có : \(\hept{\begin{cases}BF=FC\\FK//AB\end{cases}}\)
\(\Rightarrow AK=KC\)
Xét \(\Delta ABD\) có : \(\hept{\begin{cases}AE=ED\\EI//AB\end{cases}}\)
\(\Rightarrow BI=ID\)
Vậy \(\hept{\begin{cases}AK=KC\\BI=ID\end{cases}\left(đpcm\right)}\)
b ) Vì EF là đường trung bình của hình thang ABCD.
\(\Rightarrow EF=\frac{CD+AB}{2}=\frac{10+6}{8}=2\left(cm\right)\)
Mặt khác, ta có :
* EI là đường trung bình của \(\Delta ABD\)
\(\Rightarrow EI=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
* KF là đường trung bình của \(\Delta ABC\)
\(\Rightarrow KF=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
Mà : EF = EI + IK + KF
\(\Rightarrow\) IK = EF - ( EI + KF ) = 8 - ( 3 + 3 ) = 2cm.
Vậy \(\hept{\begin{cases}EI=3cm\\KF=3cm\\IK=2cm\end{cases}}\)
Chúc bạn học tốt !!!

Áp dụng định lí 1 đường trung bình của tam giác
ΔADC có E là trung điểm AD và EI song song với cạnh DC
⇒ Điểm I là trung điểm AC
ΔABC có I là trung điểm AC và FI song song với cạnh AB
⇒ điểm F là trung điểm BC
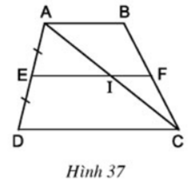
Xét ΔCAB có IF//AB
nên CF/CB=CI/CA=1/2
=>F là trung điểm của BC
Xét ΔADC có
I là trung điểm của AC
IE//DC
=>E là trung điểm của AD
Xét hình thang ABCD có
E,F lần lượt là trung điểm của AD,BC
=>EF//AB//CD
=>AE/AD=BF/BC=CF/CB